


Next: Radiation and Simple
Up: No Title
Previous: No Title
For the purposes of this work, we assume that a fractal antenna can be
formed as an array of ''small'' line elements having a fractal distribution
in space. Such description is consistent with our understanding of fractal
discharges and lightning observations as discussed by LeVine and
Meneghini [1978], Niemeyer et al. [1984], Sander
[1986], Williams [1988], and Lyons [1994]. Appendix A
develops the theory for the calculation of the fields produced by a fractal
antenna composed of small line elements and for the calculation of the array
factor in the far field of the fractal.
Fractals are characterized by their dimension. It is the key structural
parameter describing the fractal and is defined by partitioning the volume
where the fractal lies into boxes of side  . We hope that over
a few decades in
. We hope that over
a few decades in  , the number of boxes that contain at least
one of the discharge elements will scale as
, the number of boxes that contain at least
one of the discharge elements will scale as 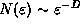 . It is easy to verify that a point will have D=0, a line will have
. It is easy to verify that a point will have D=0, a line will have 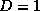 and a compact surface will have D=2 . The box counting dimension [
Ott, 1993] is then defined by
and a compact surface will have D=2 . The box counting dimension [
Ott, 1993] is then defined by
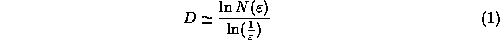
For a real discharge there is only a finite range over which the above
scaling law will apply. If  is too small, then the elements of
the discharge will look like one-dimensional line elements. Similarly, if
is too small, then the elements of
the discharge will look like one-dimensional line elements. Similarly, if  is too large, then the discharge will appear as a single
point. It is, therefore, important to compute D only in the scaling range,
which is hopefully over a few decades in
is too large, then the discharge will appear as a single
point. It is, therefore, important to compute D only in the scaling range,
which is hopefully over a few decades in  . The fractal
dimension will be an important parametrization for the fractal discharge
models that we will explore later, and will impact significantly the
intensity and spatial structure of the radiated pattern.
. The fractal
dimension will be an important parametrization for the fractal discharge
models that we will explore later, and will impact significantly the
intensity and spatial structure of the radiated pattern.
We consider a fractal antenna as a non uniform distribution of radiating
elements (Fig. 1). Each of the elements contributes to the total
radiated power density at a given point with a vectorial amplitude and
phase, i.e.
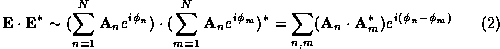
The vector amplitudes A represent the strength and orientation
of each of the individual elements, while the phases
represent the strength and orientation
of each of the individual elements, while the phases 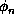 are in
general related to the spatial distribution of the individual elements over
the fractal, e.g. for an oscillating current of the form e
are in
general related to the spatial distribution of the individual elements over
the fractal, e.g. for an oscillating current of the form e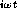 the
phases vary as
the
phases vary as 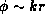 where
where 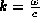 and r is the position
of the element in the fractal.
and r is the position
of the element in the fractal.
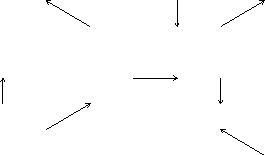
Figure 1: A spatially nonuniform distribution of radiators, each
contributiong to the total radiation field with a given phase.
In the sense of statistical optics, we can consider the ensemble average of
Eq. (2), using an ergodic principle, over the spatial
distribution 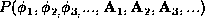 of the fractal elements [Goodman, 1985]. For
simplicity we assume that the distributions for each of the elements are
independent, and also the same, hence
of the fractal elements [Goodman, 1985]. For
simplicity we assume that the distributions for each of the elements are
independent, and also the same, hence
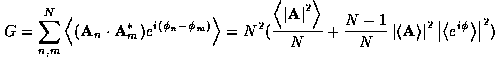
By requiring that 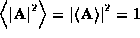 we obtain that
the ensemble average is
we obtain that
the ensemble average is
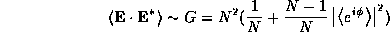
If the distribution of the phases is uniform (e.g. random) then 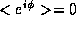 and
and 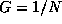 . On the other hand, if there is perfect coherence we have
. On the other hand, if there is perfect coherence we have 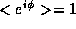 and G=1. In general, a fractal antenna will display a
power law distribution in the phases
and G=1. In general, a fractal antenna will display a
power law distribution in the phases 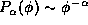 (multiplied by the factor
(multiplied by the factor 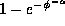 so it is finite at the
origin), where
so it is finite at the
origin), where 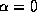 corresponds to the uniform distribution case and
corresponds to the uniform distribution case and 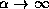 corresponds to perfect coherence. Figure 2 shows the plot of
corresponds to perfect coherence. Figure 2 shows the plot of 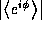 as a function of
as a function of 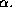 It can be seen that a power law
distribution of phases, or similarly a power law in the spatial structure,
gives rise to partial coherence.
It can be seen that a power law
distribution of phases, or similarly a power law in the spatial structure,
gives rise to partial coherence.
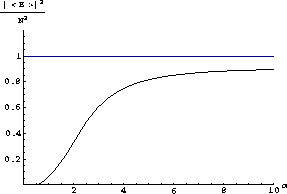
Figure 2: A plot of 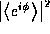 as a function of
as a function of  .
.
If the distribution of the vector amplitudes does not satisfy the above
relations, e.g. the radiators are oriented in arbitrary directions, then the
power density will be less coherent due to 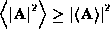 . A similar result can be achieved by having a power law
distribution in the amplitudes. In conclusion, the radiation field from a
power law distribution of phases will have a point where the phases from the
radiators will add up almost (partially) coherently showing a significant
gain over a random distribution of phases. Hence the concept of a fractal
antenna.
. A similar result can be achieved by having a power law
distribution in the amplitudes. In conclusion, the radiation field from a
power law distribution of phases will have a point where the phases from the
radiators will add up almost (partially) coherently showing a significant
gain over a random distribution of phases. Hence the concept of a fractal
antenna.
The partial coherence of the radiators depends on the spatial power law
distribution. Such a power law distribution of phases can be visualized with
the help of Cantor sets [Ott, 1993]. A family of Cantor sets is
constructed by successively removing the middle 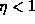 fraction from an
interval, taken as [0,1], and repeating the procedure to the remaining
intervals (see Fig. 3). At the n
fraction from an
interval, taken as [0,1], and repeating the procedure to the remaining
intervals (see Fig. 3). At the n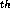 step, a radiator is
placed at the mid-point of each of the remaining intervals.
step, a radiator is
placed at the mid-point of each of the remaining intervals.
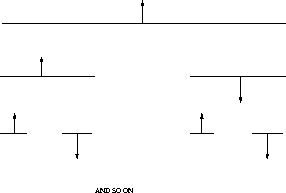
Figure 3: The construction of the fractal distribution of the radiators from
the 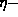 Cantor set.
Cantor set.
Note that for 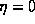 we obtain a uniform distribution of elements, but
for
we obtain a uniform distribution of elements, but
for 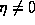 the radiators are non-uniformly distributed, and in fact
the spatial distribution follows a power law that can be described by its
fractal dimension. Suppose that for
the radiators are non-uniformly distributed, and in fact
the spatial distribution follows a power law that can be described by its
fractal dimension. Suppose that for  we require
we require 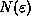 intervals to cover the fractal, then it is clear that with
intervals to cover the fractal, then it is clear that with 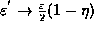 we would require
we would require 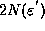 intervals to cover the fractal. But the
fractal is the same, therefore,
intervals to cover the fractal. But the
fractal is the same, therefore, 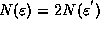 . From the scaling
. From the scaling 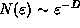 we obtain
that the dimension is given by
we obtain
that the dimension is given by

We can go further, and write a formula for the radiation field due to the 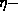 Cantor set of radiators. Note that if at the n
Cantor set of radiators. Note that if at the n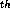 step we have
the radiators placed at the sequence of points
step we have
the radiators placed at the sequence of points 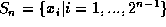 then at the n
then at the n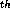 +1 step each radiator at x
+1 step each radiator at x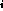 will be replaced by two
radiators at
will be replaced by two
radiators at 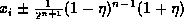 generating
the sequence
generating
the sequence 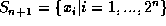 . Since we start with
. Since we start with 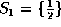 the sequences
the sequences 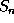 at the n
at the n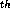 step are trivially constructed.
The radiation field (see Eq. (1)) from this
step are trivially constructed.
The radiation field (see Eq. (1)) from this 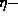 Cantor set
at the n
Cantor set
at the n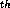 step can then be written as
step can then be written as
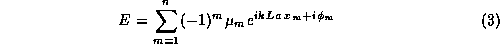
where 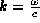 , L is the spatial extent of the fractal,
, L is the spatial extent of the fractal,  is the angular position of
the detector, and
is the angular position of
the detector, and 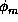 (taken as zero) is the phase of the m
(taken as zero) is the phase of the m element. The radiators are given a strength proportional to the measure
element. The radiators are given a strength proportional to the measure 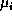 (or length) of the segment which defines it.
(or length) of the segment which defines it.
The space dependence of the radiation fields is plotted in Fig. (4)a-b for 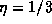 (
(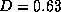 ) and
) and 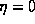 (D=1)
respectively, where the sets have been taken to the 5
(D=1)
respectively, where the sets have been taken to the 5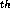 level. The most
relevant issue for our purposes is the fact that there is a direction at
which phases add coherently (partially) for
level. The most
relevant issue for our purposes is the fact that there is a direction at
which phases add coherently (partially) for 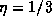 while this does not
happen for the homogeneous case
while this does not
happen for the homogeneous case 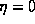 .
.
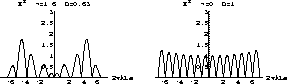
Figure 4: The spatial dependence of the radiation fields for (a) 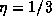 ,
,
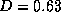 and (b)
and (b) 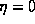 , D=1.
, D=1.
Therefore, partial coherence occurs naturally in systems that have power-law
spatial distributions. We are now ready to turn to the properties of fractal
antennae with propagating currents. Specifically, how tortuosity and
branching can increase the radiated field intensity in some locations as
compared with single dipole antennae.



Next: Radiation and Simple
Up: No Title
Previous: No Title
 . We hope that over
a few decades in
. We hope that over
a few decades in  , the number of boxes that contain at least
one of the discharge elements will scale as
, the number of boxes that contain at least
one of the discharge elements will scale as 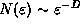 . It is easy to verify that a point will have D=0, a line will have
. It is easy to verify that a point will have D=0, a line will have 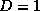 and a compact surface will have D=2 . The box counting dimension [
Ott, 1993] is then defined by
and a compact surface will have D=2 . The box counting dimension [
Ott, 1993] is then defined by
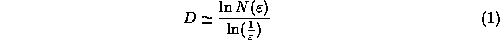
 is too small, then the elements of
the discharge will look like one-dimensional line elements. Similarly, if
is too small, then the elements of
the discharge will look like one-dimensional line elements. Similarly, if  is too large, then the discharge will appear as a single
point. It is, therefore, important to compute D only in the scaling range,
which is hopefully over a few decades in
is too large, then the discharge will appear as a single
point. It is, therefore, important to compute D only in the scaling range,
which is hopefully over a few decades in  . The fractal
dimension will be an important parametrization for the fractal discharge
models that we will explore later, and will impact significantly the
intensity and spatial structure of the radiated pattern.
. The fractal
dimension will be an important parametrization for the fractal discharge
models that we will explore later, and will impact significantly the
intensity and spatial structure of the radiated pattern.
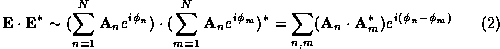
 represent the strength and orientation
of each of the individual elements, while the phases
represent the strength and orientation
of each of the individual elements, while the phases 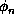 are in
general related to the spatial distribution of the individual elements over
the fractal, e.g. for an oscillating current of the form e
are in
general related to the spatial distribution of the individual elements over
the fractal, e.g. for an oscillating current of the form e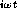 the
phases vary as
the
phases vary as 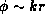 where
where 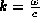 and r is the position
of the element in the fractal.
and r is the position
of the element in the fractal.

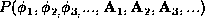 of the fractal elements [Goodman, 1985]. For
simplicity we assume that the distributions for each of the elements are
independent, and also the same, hence
of the fractal elements [Goodman, 1985]. For
simplicity we assume that the distributions for each of the elements are
independent, and also the same, hence
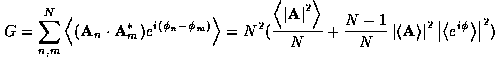
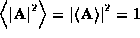 we obtain that
the ensemble average is
we obtain that
the ensemble average is
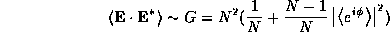
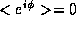 and
and 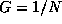 . On the other hand, if there is perfect coherence we have
. On the other hand, if there is perfect coherence we have 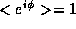 and G=1. In general, a fractal antenna will display a
power law distribution in the phases
and G=1. In general, a fractal antenna will display a
power law distribution in the phases 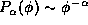 (multiplied by the factor
(multiplied by the factor 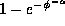 so it is finite at the
origin), where
so it is finite at the
origin), where 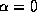 corresponds to the uniform distribution case and
corresponds to the uniform distribution case and  corresponds to perfect coherence. Figure
corresponds to perfect coherence. Figure 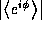 as a function of
as a function of 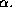 It can be seen that a power law
distribution of phases, or similarly a power law in the spatial structure,
gives rise to partial coherence.
It can be seen that a power law
distribution of phases, or similarly a power law in the spatial structure,
gives rise to partial coherence.

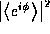 as a function of
as a function of  .
.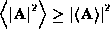 . A similar result can be achieved by having a power law
distribution in the amplitudes. In conclusion, the radiation field from a
power law distribution of phases will have a point where the phases from the
radiators will add up almost (partially) coherently showing a significant
gain over a random distribution of phases. Hence the concept of a fractal
antenna.
. A similar result can be achieved by having a power law
distribution in the amplitudes. In conclusion, the radiation field from a
power law distribution of phases will have a point where the phases from the
radiators will add up almost (partially) coherently showing a significant
gain over a random distribution of phases. Hence the concept of a fractal
antenna.
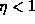 fraction from an
interval, taken as [0,1], and repeating the procedure to the remaining
intervals (see Fig.
fraction from an
interval, taken as [0,1], and repeating the procedure to the remaining
intervals (see Fig.  step, a radiator is
placed at the mid-point of each of the remaining intervals.
step, a radiator is
placed at the mid-point of each of the remaining intervals.

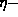 Cantor set.
Cantor set.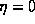 we obtain a uniform distribution of elements, but
for
we obtain a uniform distribution of elements, but
for 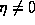 the radiators are non-uniformly distributed, and in fact
the spatial distribution follows a power law that can be described by its
fractal dimension. Suppose that for
the radiators are non-uniformly distributed, and in fact
the spatial distribution follows a power law that can be described by its
fractal dimension. Suppose that for  we require
we require 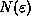 intervals to cover the fractal, then it is clear that with
intervals to cover the fractal, then it is clear that with 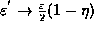 we would require
we would require 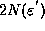 intervals to cover the fractal. But the
fractal is the same, therefore,
intervals to cover the fractal. But the
fractal is the same, therefore, 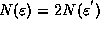 . From the scaling
. From the scaling 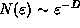 we obtain
that the dimension is given by
we obtain
that the dimension is given by

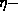 Cantor set of radiators. Note that if at the n
Cantor set of radiators. Note that if at the n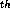 step we have
the radiators placed at the sequence of points
step we have
the radiators placed at the sequence of points 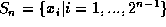 then at the n
then at the n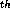 +1 step each radiator at x
+1 step each radiator at x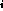 will be replaced by two
radiators at
will be replaced by two
radiators at 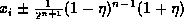 generating
the sequence
generating
the sequence 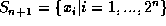 . Since we start with
. Since we start with 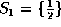 the sequences
the sequences 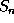 at the n
at the n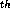 step are trivially constructed.
The radiation field (see Eq. (
step are trivially constructed.
The radiation field (see Eq. (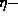 Cantor set
at the n
Cantor set
at the n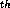 step can then be written as
step can then be written as
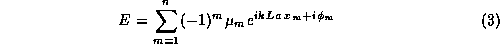
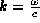 , L is the spatial extent of the fractal,
, L is the spatial extent of the fractal,  is the angular position of
the detector, and
is the angular position of
the detector, and 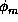 (taken as zero) is the phase of the m
(taken as zero) is the phase of the m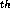 element. The radiators are given a strength proportional to the measure
element. The radiators are given a strength proportional to the measure 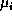 (or length) of the segment which defines it.
(or length) of the segment which defines it.
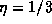 (
(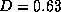 ) and
) and 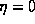 (D=1)
respectively, where the sets have been taken to the 5
(D=1)
respectively, where the sets have been taken to the 5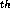 level. The most
relevant issue for our purposes is the fact that there is a direction at
which phases add coherently (partially) for
level. The most
relevant issue for our purposes is the fact that there is a direction at
which phases add coherently (partially) for 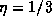 while this does not
happen for the homogeneous case
while this does not
happen for the homogeneous case 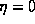 .
.
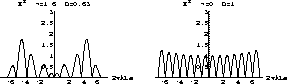
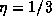 ,
,
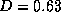 and (b)
and (b) 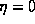 , D=1.
, D=1.