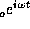Another element in understanding fractal antennae is the concept of
branching. Take the simple branching element shown in Fig. 9
where the current is divided between the two branching elements. We can
compute the radiation field, for a propagating current I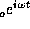
,
as
where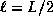 
and 
is the variation from the single
dipole, i.e. we recover the dipole as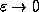 
.
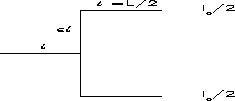
Figure 9: A simple branching situation in which we distribute the current
among the branching elements.
Again, the analysis can be simplified in the limit for small 
,
i.e.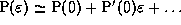 
. Of course P(0) is the dipole contribution, and 
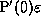is the change in the radiated power
density due to the line branching. The dipole has a maximum in the radiated
power density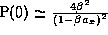 
, while
the branching contribution goes as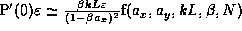 
. The function f depends on the given parameters, but
its maximum is of the order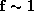 
with clear regions in 
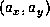where it is positive. Therefore, the branching process can give
rise to an increase in the radiated power density at certain position. Of
course this increase is due to the increase in the path length. This effect
will saturate as 
is increased passed one, since then the
strongest contribution will come from the dipole radiator given by 2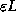
.
A interesting and manageable broadband antenna can be described in terms of
the Weierstrass functions [Werner and Werner, 1995]. We take
successive branching elements, as shown in Fig. 10a, where we
distribute the current at each branching point so that the branching element
keeps a fraction 
of the current. The n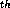
branching element is
displaced by a factor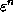 
with respect to the origin. If we
concentrate only on the contribution from the last branching set, as shown
in Fig. 10a, we can write the field as
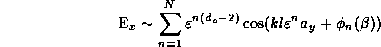
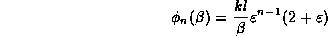
where we have redefined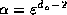 
and a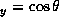
. In the limit 
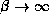and N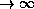
we
obtain the Weierstrass function that is continuous but not differentiable,
i.e. is a fractal, and furthermore, its dimension in the sense given by Eq.
( 1) is d
. For the purpose of illustration we truncate the
above sum to N=8. In Fig. 10b, we show the dependence of the
field as a function of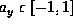 
with a
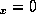for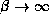 
. The parameters values are shown in the figure caption.
Figure 10c shows the gain factor given by
as a function of the dimension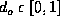 
. We chose this range
since the fractal already has a dimension 1 in the perpendicular directions,
i.e. D=1+d
.
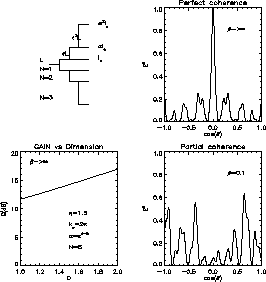
Figure 10: The branching process to produce a Weierstrass radiation pattern.
(a) The brunching process with the branching length increasing as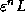 
and the current decreasing as 
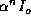. (b) the
radiation pattern with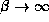 
given perfect coherence.
(c) The gain vs the dimension. It also contains the parameters used in all 3
figures. (d) Patial coherence for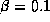 
.
Note the increase in the gain as a function of dimension. In general, there
is an optimal value of D that generates the highest power density and that
does not necessarily has to be for D=2. In Fig. 10b all the
elements from the antenna add up coherently at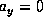 
, hence providing
perfect coherence. For a finite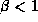 
the propagation brings a
different phase shift at each element. Figure 10d shows the
effect for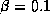 
as a function of 
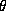. Note that at no point
there is perfect coherence, but there is clear partial coherence. The peak
value of E
is actually sensitive to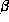 
.
Even though fractal antennae naturally lead to the concept of an increase in the peak radiated power, it also has a second important consequence due to branching. As we have seen in the case of the Wiertrauss function, fractal antennae naturally result in the generation of a spatial structure in the radiated power density. This interplay between the spatial structure and the increase in the peak radiated power are the essential ingredients of fractal antennae and why they are so important. A clear example can be illustrated in Fig. 10d where there are multiple relevant peaks of the radiated power in space.
