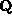 [
Marion and Heald, 1980] that is related to the current density
[
Marion and Heald, 1980] that is related to the current density  and the charge density
and the charge density 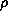 as
as
The fields from a line element can be solve with the help of the Hertz
Vector [Marion and Heald, 1980]. In order to solve Maxwell's
equations we define, in empty space, the vector function 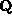 [
Marion and Heald, 1980] that is related to the current density
[
Marion and Heald, 1980] that is related to the current density  and the charge density
and the charge density 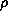 as
as


Note that 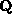 solves the continuity equation trivially, and
furthermore, it can be used to define another vector function, namely the
Hertz vector
solves the continuity equation trivially, and
furthermore, it can be used to define another vector function, namely the
Hertz vector  as
as

where the fields are then defined as


The time-Fourier transformed Maxwell's equations, with 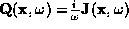 and
and  can be solved with the help of the Hertz vector
can be solved with the help of the Hertz vector 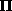 ,
,

where the line element has orientation 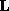 and length L, and is
parametrized by
and length L, and is
parametrized by 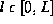 . Values with the hat
. Values with the hat  indicate unit vectors, variables in bold indicate vectors,
indicate unit vectors, variables in bold indicate vectors,  is the
frequency,
is the
frequency,  . The time dependence can be found by inverting
the above equation.
. The time dependence can be found by inverting
the above equation.