


Next: The Far field
Up: No Title
Previous: Fields from a
A current pulse propagates with speed 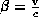 along a
fractal structure. At the n
along a
fractal structure. At the n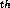 line element with orientation
line element with orientation 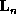 and length
and length 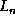 , which is parametrized by
, which is parametrized by 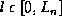 , the
current is given by
, the
current is given by  where
where 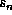 is the path length along the fractal (or if you prefer a phase shift). The
radiation field is the superposition, with the respective phases, of the
small line current elements that form the fractal. For a set
is the path length along the fractal (or if you prefer a phase shift). The
radiation field is the superposition, with the respective phases, of the
small line current elements that form the fractal. For a set  of line elements, such as shown in
the example diagram of Fig. 25, the Hertz vector is given by
of line elements, such as shown in
the example diagram of Fig. 25, the Hertz vector is given by
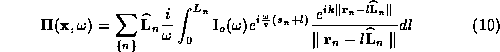
where 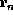 is the vector from the beginning of the
is the vector from the beginning of the 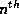 line
element to the field position
line
element to the field position  ,
,  is the frequency and
is the frequency and  .
.

Figure 25: A diagram that explains all the variables and coefficients
We must realize that in general Eq. 10 for  is
very complicated, but we are interested in the far field of the small line
elements (
is
very complicated, but we are interested in the far field of the small line
elements ( ). Therefore, we can take the far field approximation of
the small line elements to obtain a closed form solution for the Fourier
transformed fields as
). Therefore, we can take the far field approximation of
the small line elements to obtain a closed form solution for the Fourier
transformed fields as
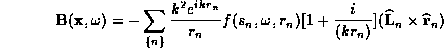

where the geometric factor is given by
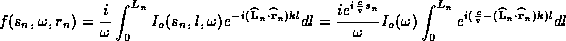
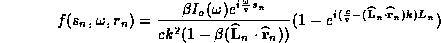
Note that even though we are in the far field of the small line elements, we
can be in fact in the intermediate field with respect to the global fractal
structure. Therefore, phase correlations over the fractal can be extremely
relevant, and produce spatially nonuniform radiation fields. We then invert
the Fourier transform of the field to real time and obtain the
spatio-temporal radiation pattern due to the fractal discharge structure
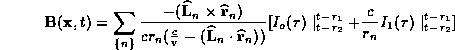
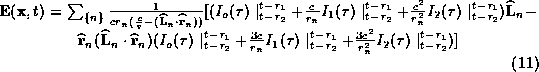
where

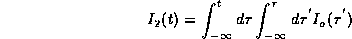
can be calculated exactly for the current described above, and where

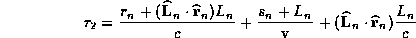
The value of 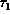 and
and  correspond to the causal time delays
from the two end points of the line element.
correspond to the causal time delays
from the two end points of the line element.
Before finishing this section we want to mention that there is an inherent
symmetry in the radiation fields. In general we will assume that the current
is given by 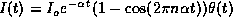 where
where
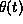 is the step function, and
is the step function, and 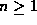 . Note that the total charge
discharged by this current is Q=
. Note that the total charge
discharged by this current is Q=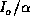 where
where 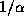 is the decay
time of the current. But since the current propagates along the fractal, the
radiation fields at a given position in space will last for a time given by
is the decay
time of the current. But since the current propagates along the fractal, the
radiation fields at a given position in space will last for a time given by 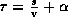 where s is the largest path length along
the fractal. The fields are invariant as long as
where s is the largest path length along
the fractal. The fields are invariant as long as  ,
,  and
and  are kept constant in the
transformation. Such scaling can become relevant in studying the properties
of radiation fields from fractal antennae.
are kept constant in the
transformation. Such scaling can become relevant in studying the properties
of radiation fields from fractal antennae.
In general we will use the power density  where 1/
where 1/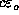 is the impedance of free space, as a natural
description for the amount of power radiated through a cross-sectional area.
is the impedance of free space, as a natural
description for the amount of power radiated through a cross-sectional area.



Next: The Far field
Up: No Title
Previous: Fields from a
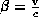 along a
fractal structure. At the n
along a
fractal structure. At the n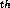 line element with orientation
line element with orientation 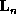 and length
and length 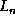 , which is parametrized by
, which is parametrized by 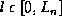 , the
current is given by
, the
current is given by  where
where 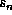 is the path length along the fractal (or if you prefer a phase shift). The
radiation field is the superposition, with the respective phases, of the
small line current elements that form the fractal. For a set
is the path length along the fractal (or if you prefer a phase shift). The
radiation field is the superposition, with the respective phases, of the
small line current elements that form the fractal. For a set  of line elements, such as shown in
the example diagram of Fig. 25, the Hertz vector is given by
of line elements, such as shown in
the example diagram of Fig. 25, the Hertz vector is given by
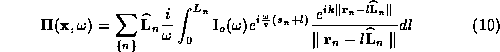
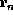 is the vector from the beginning of the
is the vector from the beginning of the 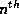 line
element to the field position
line
element to the field position  ,
,  is the frequency and
is the frequency and  .
.

 is
very complicated, but we are interested in the far field of the small line
elements (
is
very complicated, but we are interested in the far field of the small line
elements ( ). Therefore, we can take the far field approximation of
the small line elements to obtain a closed form solution for the Fourier
transformed fields as
). Therefore, we can take the far field approximation of
the small line elements to obtain a closed form solution for the Fourier
transformed fields as
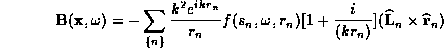

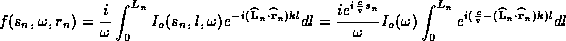
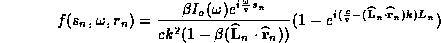
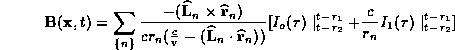
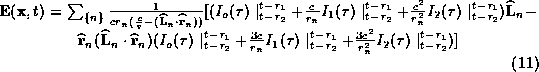

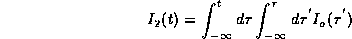

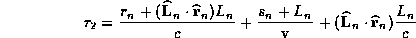
 and
and  correspond to the causal time delays
from the two end points of the line element.
correspond to the causal time delays
from the two end points of the line element.
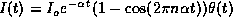 where
where
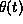 is the step function, and
is the step function, and 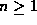 . Note that the total charge
discharged by this current is Q=
. Note that the total charge
discharged by this current is Q=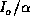 where
where 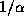 is the decay
time of the current. But since the current propagates along the fractal, the
radiation fields at a given position in space will last for a time given by
is the decay
time of the current. But since the current propagates along the fractal, the
radiation fields at a given position in space will last for a time given by 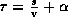 where s is the largest path length along
the fractal. The fields are invariant as long as
where s is the largest path length along
the fractal. The fields are invariant as long as  ,
,  and
and  are kept constant in the
transformation. Such scaling can become relevant in studying the properties
of radiation fields from fractal antennae.
are kept constant in the
transformation. Such scaling can become relevant in studying the properties
of radiation fields from fractal antennae.
 where 1/
where 1/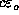 is the impedance of free space, as a natural
description for the amount of power radiated through a cross-sectional area.
is the impedance of free space, as a natural
description for the amount of power radiated through a cross-sectional area.