


Next: Computing the Fields
Up: Modeling Lightning as
Previous: Modeling Lightning as
We want to generate a fractal model that can be parametrized by its fractal
dimension. For this purpose, we follow Niemeyer et al. [1984] who
proposed a two dimensional stochastic dielectric discharge model that
naturally leads to fractal structures. In this model the fractal dimension D
can be easily parametrized by a parameter  . Femia et al. [1993] found
experimentally that the propagating stochastic Lichtenberg pattern is
approximately an equipotential. Then, the idea is to create a discrete
discharge pattern that grows stepwise by adding an adjacent grid point to
the discharge pattern generating a new bond. The new grid point, being part
of the discharge structure, will have the same potential as the discharge
pattern. Such local change will affect the global potential configuration,
see Fig. 13.
. Femia et al. [1993] found
experimentally that the propagating stochastic Lichtenberg pattern is
approximately an equipotential. Then, the idea is to create a discrete
discharge pattern that grows stepwise by adding an adjacent grid point to
the discharge pattern generating a new bond. The new grid point, being part
of the discharge structure, will have the same potential as the discharge
pattern. Such local change will affect the global potential configuration,
see Fig. 13.
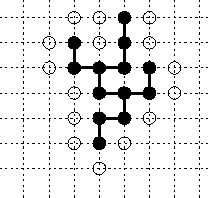
Figure 13: Diagram of the discrete discharge model.
The potential for the points not on the discharge structure is calculated by
iterating the discrete two dimensional Laplace's equation

until it converges. This method reproduces the global influence of a given
discharge pattern as it expands. The discharge pattern evolves by adding an
adjacent grid point. The main assumption here is that an adjacent grid point
denoted by (l,m) has a probability of becoming part of the discharge pattern
proportional to the  power of the local electric field, which
translates to
power of the local electric field, which
translates to

in terms of the local potential. Here we have assumed that the potential at
the discharge is zero. The structure generated for 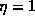 , corresponding
to a Lichtenberg pattern, is shown in Fig. 14.
, corresponding
to a Lichtenberg pattern, is shown in Fig. 14.

Figure 14: Fractal discharge generated with 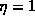 .
.
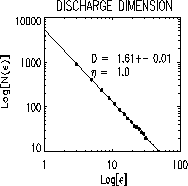
Figure 15: The plot of  vs
vs  for
for  .
.
The color coding corresponds to the potential. Figure 15 shows a
plot of  vs.
vs. 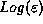 for the fractal discharge
of Fig. 14, i.e.
for the fractal discharge
of Fig. 14, i.e.  . Again the scaling behavior only
occurs over a few decades, but it is very clear. The dimension of this
structure is
. Again the scaling behavior only
occurs over a few decades, but it is very clear. The dimension of this
structure is 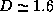 .
.

Figure 16: The dimension of the stochastic model as a function of  with
the estimated error bars.
with
the estimated error bars.
Note that this model, and also the dimension of the discharge, is
parametrized by  . Intuitively we expect that when
. Intuitively we expect that when 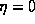 the
discharge will have the same probability of propagating in any direction,
therefore, the discharge will be a compact structure with a dimension D=2.
If
the
discharge will have the same probability of propagating in any direction,
therefore, the discharge will be a compact structure with a dimension D=2.
If 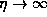 then the discharge will go in only one
direction, hence D=1. Between these two limits, the dimension will be the
function
then the discharge will go in only one
direction, hence D=1. Between these two limits, the dimension will be the
function 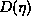 shown in Fig 16. As an example the
corresponding structure generated for
shown in Fig 16. As an example the
corresponding structure generated for  (Fig 17) has a
dimension of
(Fig 17) has a
dimension of 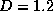 .
.
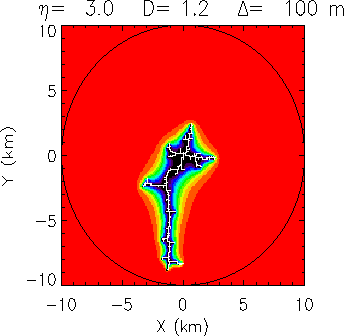
Figure 17: Fractal discharge generated for 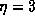 .
.
To compute the radiated fields, we must describe the current along each of
the segments of the fractal discharge. We start with a charge 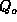 at the
center of the discharge. The current is then discharged along each of the
dendritic arms. At each branching point we chose to ensure conservation of
current, but intuitively we know that a larger fraction of the current will
propagate along the longest arm. Suppose that a current
at the
center of the discharge. The current is then discharged along each of the
dendritic arms. At each branching point we chose to ensure conservation of
current, but intuitively we know that a larger fraction of the current will
propagate along the longest arm. Suppose that a current 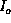 arrives at a
branching point, and if
arrives at a
branching point, and if 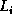 is the longest distance along the
is the longest distance along the 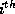 branching arm, we intuitively expect that the current on the
branching arm, we intuitively expect that the current on the 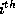 arm
should be proportional to
arm
should be proportional to  . Therefore, we satisfy charge (or
current) conservation if the current along the
. Therefore, we satisfy charge (or
current) conservation if the current along the 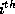 branching arm is
branching arm is




Next: Computing the Fields
Up: Modeling Lightning as
Previous: Modeling Lightning as
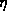 . Femia et al. [1993] found
experimentally that the propagating stochastic Lichtenberg pattern is
approximately an equipotential. Then, the idea is to create a discrete
discharge pattern that grows stepwise by adding an adjacent grid point to
the discharge pattern generating a new bond. The new grid point, being part
of the discharge structure, will have the same potential as the discharge
pattern. Such local change will affect the global potential configuration,
see Fig. 13.
. Femia et al. [1993] found
experimentally that the propagating stochastic Lichtenberg pattern is
approximately an equipotential. Then, the idea is to create a discrete
discharge pattern that grows stepwise by adding an adjacent grid point to
the discharge pattern generating a new bond. The new grid point, being part
of the discharge structure, will have the same potential as the discharge
pattern. Such local change will affect the global potential configuration,
see Fig. 13.


 power of the local electric field, which
translates to
power of the local electric field, which
translates to

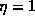 , corresponding
to a Lichtenberg pattern, is shown in Fig.
, corresponding
to a Lichtenberg pattern, is shown in Fig. 
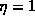 .
.
 vs
vs  for
for  .
. vs.
vs. 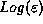 for the fractal discharge
of Fig.
for the fractal discharge
of Fig.  . Again the scaling behavior only
occurs over a few decades, but it is very clear. The dimension of this
structure is
. Again the scaling behavior only
occurs over a few decades, but it is very clear. The dimension of this
structure is 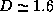 .
.

 with
the estimated error bars.
with
the estimated error bars. . Intuitively we expect that when
. Intuitively we expect that when 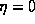 the
discharge will have the same probability of propagating in any direction,
therefore, the discharge will be a compact structure with a dimension D=2.
If
the
discharge will have the same probability of propagating in any direction,
therefore, the discharge will be a compact structure with a dimension D=2.
If 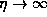 then the discharge will go in only one
direction, hence D=1. Between these two limits, the dimension will be the
function
then the discharge will go in only one
direction, hence D=1. Between these two limits, the dimension will be the
function 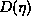 shown in Fig
shown in Fig  (Fig
(Fig 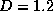 .
.

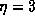 .
. 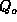 at the
center of the discharge. The current is then discharged along each of the
dendritic arms. At each branching point we chose to ensure conservation of
current, but intuitively we know that a larger fraction of the current will
propagate along the longest arm. Suppose that a current
at the
center of the discharge. The current is then discharged along each of the
dendritic arms. At each branching point we chose to ensure conservation of
current, but intuitively we know that a larger fraction of the current will
propagate along the longest arm. Suppose that a current 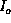 arrives at a
branching point, and if
arrives at a
branching point, and if 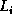 is the longest distance along the
is the longest distance along the 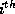 branching arm, we intuitively expect that the current on the
branching arm, we intuitively expect that the current on the 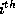 arm
should be proportional to
arm
should be proportional to  . Therefore, we satisfy charge (or
current) conservation if the current along the
. Therefore, we satisfy charge (or
current) conservation if the current along the 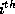 branching arm is
branching arm is
