 generating radiation fields. The radiation field is the superposition,
with the respective phases, of the small line current elements. The
intracloud current pulse is taken as a series of train pulses that propagate
along the arms of the antenna
generating radiation fields. The radiation field is the superposition,
with the respective phases, of the small line current elements. The
intracloud current pulse is taken as a series of train pulses that propagate
along the arms of the antenna
A current pulse propagates along the horizontal (in the x-y plane) 2
dimensional fractal discharge structure, e.g.  generating radiation fields. The radiation field is the superposition,
with the respective phases, of the small line current elements. The
intracloud current pulse is taken as a series of train pulses that propagate
along the arms of the antenna
generating radiation fields. The radiation field is the superposition,
with the respective phases, of the small line current elements. The
intracloud current pulse is taken as a series of train pulses that propagate
along the arms of the antenna
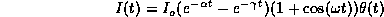
with  and
and  as the step function. Here n
as the step function. Here n represent the number of oscillations during the decay time scale 1/
represent the number of oscillations during the decay time scale 1/ . We chose the decay parameters as
. We chose the decay parameters as 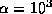 s
s and
and 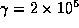 s
s , hence
, hence  , which
correspond to realistic parameters for lightning [Uman, 1987]. The
total charge discharged is then
, which
correspond to realistic parameters for lightning [Uman, 1987]. The
total charge discharged is then  , which for
, which for  gives
gives 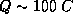 . As we have seen before, we require
. As we have seen before, we require 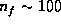 to
create the spatial structures so that the exponential decay
to
create the spatial structures so that the exponential decay 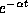 can be considered as the envelope of the oscillating part.
can be considered as the envelope of the oscillating part.
On a given position the time dependence of the field intensity E has a
fractal structure, as it is shown in Fig. 18a for the stochastic
discharge model with
has a
fractal structure, as it is shown in Fig. 18a for the stochastic
discharge model with 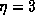 . The frequency spectrum of the electric field
is shown in Fig. 18b. It is very important to realize that the
relevant frequencies are below a few hundred kHz. By restricting the field
frequencies to below a few hundred kHz, the analysis is greatly simplified,
since then the conductivity and dielectric tensors can be considered as
independent of time in the lower ionosphere (see Appendix B).
. The frequency spectrum of the electric field
is shown in Fig. 18b. It is very important to realize that the
relevant frequencies are below a few hundred kHz. By restricting the field
frequencies to below a few hundred kHz, the analysis is greatly simplified,
since then the conductivity and dielectric tensors can be considered as
independent of time in the lower ionosphere (see Appendix B).
The large conductivity of the ground at these frequencies can be included by
assuming to first order an image discharge of opposite current below a
perfectly conductive plane. The primary discharge is taken to be at z km above the ground. This parameter is not very relevant, since we are
interested in the field at heights of about
km above the ground. This parameter is not very relevant, since we are
interested in the field at heights of about  km, therefore, moving
the discharge from 5 to 10 km will only change the field strength by a
marginal 10%.
km, therefore, moving
the discharge from 5 to 10 km will only change the field strength by a
marginal 10%.

Figure 18: (a) The field power density due to the stochastic discharge model
at a given position as a function time (b) and the frequency spectrum of the
field.