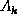For a 2-dimensional fractal structure, we expect that the strength of the
radiated power density depends on the fractal structure, i.e. its fractal
dimension. If the strength of the k Fourier component is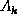 
then the
field in the far field [ Jackson 1975] at r along the axis of the
fractal will be given by
where d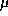
(the fractal measure) is the contribution of the fractal from
a given polar position (
,
). 
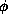is the phase
contribution from the elements of the fractal at position (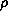
,
)
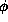and in the far field should be proportional to the direction of the local
current. Note that a radially propagating uniform 2 dimensional current
structure will generate no field at the axis since contributions to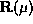 
from different parts of the fractal will cancel each other.
The cross section of the fractal at a given radius 
will resemble a
Cantor set in 
, and the phase contribution will
be given by 
which
will be finite for an asymmetrical fractal. The integration can be carried
as a Lebesgue integral or as a Riemann-Stieltjes integral over this
pseudo-Cantor set [Royden, 1963]. Note that if the fractal is
uniformly distributed along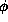 
, corresponding to D=2, then 
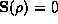. Similarly, for a delta function at 
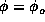corresponding
to D=1, 
gives a positive contribution.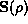 
is a very complicated function that depends on the details of the
current distribution along the fractal. In an average sense we can suppose
that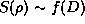 
where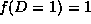 
and 
but f can be
greater than one for other values as has been investigated in previous
sections when branching and propagation occurs. Therefore,
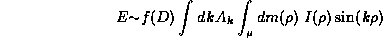
where dm(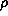
) represents the amount of the fractal between 
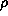and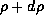 
and I(
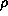) is the averaged current over 
at radius 
. A fractal will have a mass up to a radius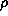 
given by 
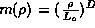by noting that a 2 dimensional antenna will have
more elements than a one dimensional fractal. In general, due to the
branching process, some of the current does not reach the radius R. But for
simplicity, if all of the current reaches the end of the fractal at radius
R, then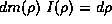 
. In such case, the above integral gives
Note that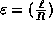 
in some sense selects the Fourier
component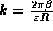 
which has a strength 
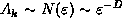. The integral over k gives 
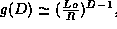therefore, the field is given by
which shows that the field has a maximum value at a specific value of 
since 
decreases and 
increases with D
respectively.
On the other hand, the Rayleigh length, the distance beyond which the field
start decaying to their far field values, behaves as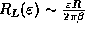 
for a given 
. Red sprites
occur at a height 
km, therefore, for 
elements with sizes smaller than 
do not contribute to the
field, i.e. as we increase z we wash out the information of increasingly
larger spatial scales of the fractal. It is the power law dependence, as
specified by the fractal dimension, that determine the field pattern.
Even though, the radiation pattern will depend on the details of the fractal
structure, we expect that the most relevant parameter in determining the
radiation pattern will be the fractal dimension, as found by Myers et al.
[1990] for simple fractals. There is an interplay between the dimension and
the spatial structure of the radiation pattern. For a dimension close to 
or 
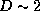, there will be no significant spatial structure. While
an intermediate dimension can produce a significant spatial structure.
