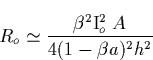The fields from a line element can be solve with the help of the Hertz
Vector [Marion and Heald, 1980]. In order to solve Maxwell's
equations we define, in empty space, the vector function ![]() [
Marion and Heald, 1980] that is related to the current density
[
Marion and Heald, 1980] that is related to the current density ![]() and the charge density
and the charge density ![]() as
as

![]()
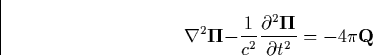
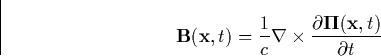
![]()
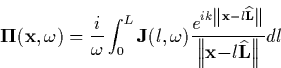 |
(24) |
A current pulse propagates with speed ![]() along a
fractal structure. At the nth line element with orientation
along a
fractal structure. At the nth line element with orientation ![]() and length Ln, which is parametrized by
and length Ln, which is parametrized by ![]() , the
current is given by
, the
current is given by ![]() where sn
is the path length along the fractal (or if you prefer a phase shift). The
radiation field is the superposition, with the respective phases, of the
small line current elements that form the fractal. For a set
where sn
is the path length along the fractal (or if you prefer a phase shift). The
radiation field is the superposition, with the respective phases, of the
small line current elements that form the fractal. For a set ![]() of line elements, such as shown in
the example diagram of Fig. A.1, the Hertz vector is given by
of line elements, such as shown in
the example diagram of Fig. A.1, the Hertz vector is given by
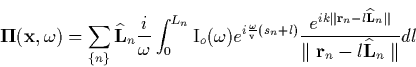 |
(25) |
 \end{displaymath}](img516.gif)
![\begin{displaymath}
\begin{array}
{c}
\mathbf{E}(\mathbf{x},\omega )=-\sum_{\{n\...
...f{r}}
_n)(1+\frac{3i}{(kr_n)}+\frac{3i^2}{(kr_n)^2}]\end{array}\end{displaymath}](img517.gif)

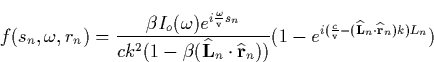
![\begin{displaymath}
\mathbf{B}(\mathbf{x},t)=\sum_{\{n\}}\frac{-(\widehat{\mathb...
...-\tau
_1}+\frac c{r_n}I_1(\tau )\mid _{t-\tau _2}^{t-\tau _1}] \end{displaymath}](img520.gif)
![\begin{displaymath}
\begin{array}
{c}
\mathbf{E}(\mathbf{x},t)=\sum_{\{n\}}\frac...
...c^2}{r_n^2}I_2(\tau )\mid _{t-\tau
_2}^{t-\tau _1})]\end{array}\end{displaymath}](img521.gif) |
(26) |
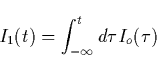
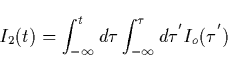

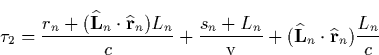
Before finishing this section we want to mention that there is an inherent
symmetry in the radiation fields. In general we will assume that the current
is given by ![]() where
where
![]() is the step function, and
is the step function, and ![]() . Note that the total charge
discharged by this current is Q=
. Note that the total charge
discharged by this current is Q=![]() where
where ![]() is the decay
time of the current. But since the current propagates along the fractal, the
radiation fields at a given position in space will last for a time given by
is the decay
time of the current. But since the current propagates along the fractal, the
radiation fields at a given position in space will last for a time given by ![]() where s is the largest path length along
the fractal. The fields are invariant as long as
where s is the largest path length along
the fractal. The fields are invariant as long as ![]() ,
, ![]() and
and ![]() are kept constant in the
transformation. Such scaling can become relevant in studying the properties
of radiation fields from fractal antennae.
are kept constant in the
transformation. Such scaling can become relevant in studying the properties
of radiation fields from fractal antennae.
In general we will use the power density ![]() where 1/
where 1/![]() is the impedance of free space, as a natural
description for the amount of power radiated through a cross-sectional area.
is the impedance of free space, as a natural
description for the amount of power radiated through a cross-sectional area.
The far field is approximately given by
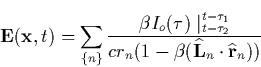 |
(27) |
In general we are going to use a current pulse defined as ![]() with
with ![]() and
and ![]() as the step function. Here nf
represent the number of oscillations during the decay time scale 1/
as the step function. Here nf
represent the number of oscillations during the decay time scale 1/![]() . We chose the decay parameters as
. We chose the decay parameters as ![]() s-1 and
s-1 and ![]() s-1, hence
s-1, hence ![]() , which correspond to
realistic parameters for lightning [Uman, 1987].
, which correspond to
realistic parameters for lightning [Uman, 1987].
As a measure of the amount of energy radiated to a given point in the far
field, we can define an array factor as ![]() From Eq. (A.4 ) we can write this array factor as
From Eq. (A.4 ) we can write this array factor as
![\begin{displaymath}
R\simeq \frac{\beta ^2\zeta ^2}{4(4+5\zeta ^2+\zeta ^4)}\sum...
...)r_nr_m}\{f[\left\vert \tau _n^f-\tau _m^f\right\vert
,\zeta ]+\end{displaymath}](img539.gif)
![\begin{displaymath}
f[\left\vert \tau _n^i-\tau _m^i\right\vert ,\zeta ]-f[\left...
...,\zeta ]-f[\left\vert \tau _n^i-\tau _m^f\right\vert ,\zeta ]\}\end{displaymath}](img540.gif) |
(28) |
![]()