Next: Population of N2 Levels
Previous: Fields from a Fractal
Once we have the fractal discharge structure, we must consider the
propagation of the lightning related electromagnetic fields in the lower
ionosphere. As the field propagate into lower ionosphere self-absorption
must be considered. The fields energize the electrons generating highly
non-Gaussian electron distribution functions. The electron energization is
computed with the help of a Fokker-Planck code. This Fokker-Planck code
include inelastic loses due to collisions with the neutrals. This is how the
fields give energy to the medium. Such inelastic losses will produce the
emissions. The present model consists of a plasma formation simulation and a
field propagation simulation. Together they calculate self-consistently the
propagation through the ionosphere by electromagnetic fields due to the
lightning discharge, which for our purposes is fractal.
As the lightning related fields propagate in the upper atmosphere and lower
ionosphere, the field changes the properties of the medium by heating the
electrons and therefore inducing self-absorption. The electromagnetic field
propagation is described by Maxwell's equations. We closely follow [ Gurevich 1978] and write Maxwell's equations as
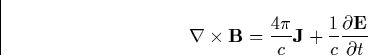



this form will be specially relevant for our further studies. The medium is
incorporated as
| 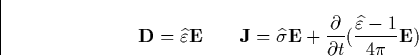 |
(29) |
where 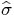 and
and 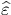 are the conductivity
and dielectric operators of the plasma, and in general depend on the field
are the conductivity
and dielectric operators of the plasma, and in general depend on the field 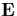 . The nonlinear wave equation describing E is then given by
. The nonlinear wave equation describing E is then given by
| 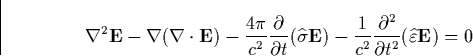 |
(30) |
Suppose we can assume that  and
and  reach a steady state faster than the relevant time evolution of Eq. (B.2), as it will occur in our case, then a wave incident at the boundary
preserves the frequency
reach a steady state faster than the relevant time evolution of Eq. (B.2), as it will occur in our case, then a wave incident at the boundary
preserves the frequency 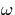 [Gurevich 1978]. In this approximation the
wave equations simplifies as
[Gurevich 1978]. In this approximation the
wave equations simplifies as
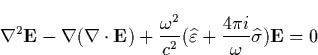
To get an idea of how the field propagates through the plasma we make the
following assumptions: (1) we take 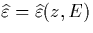 and
and 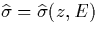 , (2)
, (2) 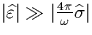 .Furthermore, if we assume a normal polarization of the wave, we then obtain
.Furthermore, if we assume a normal polarization of the wave, we then obtain
| 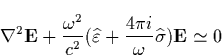 |
(31) |
The solution in this ray approximation is then written as
| ![\begin{displaymath}
\mathbf{E}(s,t)\simeq \frac{\mathbf{E}(0,t-\frac sc)}{s^2}\t...
..._{\mathbf{s}}[i\widehat{n}-\widehat{\Gamma }]\cdot d\mathbf{s}}\end{displaymath}](img560.gif) |
(32) |
where 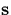 is the path of the ray. By applying this solution to Eq.
( B.3) we obtain
is the path of the ray. By applying this solution to Eq.
( B.3) we obtain

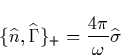
where {}+ is the anticommutator. We have assumed that
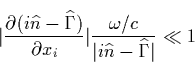
Equation (B.4) is the solution to Maxwell's equations and will be
used to describe the propagation and absorption of the fields generated by
the fractal antenna. We must still estimate the dependence of 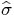 and
and 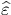 on the field E and the validity of
the independence of
on the field E and the validity of
the independence of 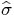 and
and 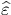 in
time. Again following [Gurevich 1978] we will estimate the
dependence of the
in
time. Again following [Gurevich 1978] we will estimate the
dependence of the 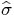 and
and 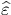 on the
field strength by looking at the plasma average velocity and energy. When
the field effects become important we will see later that the electron
distribution will have a strong directional component with the average
plasma velocity
on the
field strength by looking at the plasma average velocity and energy. When
the field effects become important we will see later that the electron
distribution will have a strong directional component with the average
plasma velocity 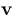 given by
given by
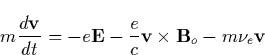
where 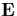 is the oscillating field, and
is the oscillating field, and 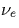 the averaged
collisional frequency with the neutrals. Only collisions with neutrals are
relevant at these heights. Similarly, we don't consider transport effects in
this region
the averaged
collisional frequency with the neutrals. Only collisions with neutrals are
relevant at these heights. Similarly, we don't consider transport effects in
this region 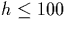 km. Note that without fields, v(t)=
v
km. Note that without fields, v(t)=
v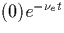 , therefore, the plasma velocity reaches a steady
state velocity in
, therefore, the plasma velocity reaches a steady
state velocity in 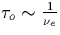 . For the region of interest,
. For the region of interest,
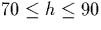 km, the background electron-neutral collisional frequency
is
km, the background electron-neutral collisional frequency
is 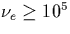 Hz and increases in the presence of an electric field.
For the case of an oscillating field
Hz and increases in the presence of an electric field.
For the case of an oscillating field 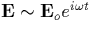 and a constant magnetic field
and a constant magnetic field 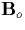 the velocity of the plasma
is given by
the velocity of the plasma
is given by
| ![\begin{displaymath}
\mathbf{v}_e=\frac{eE_o}{m[\Omega _B^2+(i\omega -\nu _e)^2]}...
...}}+\Omega _B(\widehat{\mathbf{e}}\times \widehat{\mathbf{b}})\}\end{displaymath}](img575.gif) |
(33) |
where 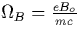 ,
, 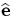 is the unit vector
in the direction of
is the unit vector
in the direction of 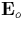 and
and 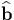 is the unit
vector in the direction of
is the unit
vector in the direction of 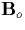 . As it can be seen in Eq. (B.1), we can obtain
. As it can be seen in Eq. (B.1), we can obtain 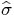 and
and 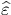 from the plasma current
from the plasma current
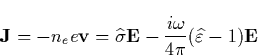
The explicit formulas of 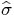 and
and 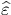 are not very illuminating, but we are interested in the case in which
are not very illuminating, but we are interested in the case in which 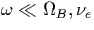 under the influence of the field. Let's define
under the influence of the field. Let's define 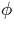 to be the angle between the magnetic field and the horizontal. In
this approximation the conductivity tensor is
to be the angle between the magnetic field and the horizontal. In
this approximation the conductivity tensor is
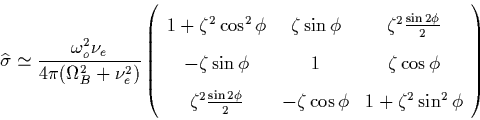
and the dielectric tensor is
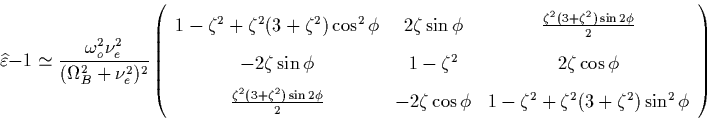
where 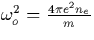 is the electron plasma frequency,
and
is the electron plasma frequency,
and 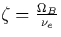 . If we take the angle
. If we take the angle 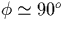 and since the electric fields are mostly horizontal for a horizontal
fractal discharge, we can finally obtain that
and since the electric fields are mostly horizontal for a horizontal
fractal discharge, we can finally obtain that
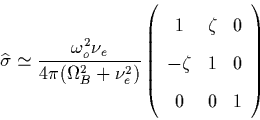
If we do not consider the diffraction effects so that 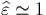 (for
(for 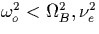 ), then
), then
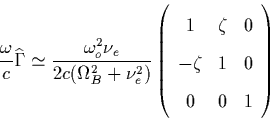
Therefore, the field power density behaves as
| 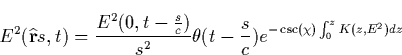 |
(34) |
where K(z,E2)= 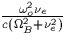 ,
, 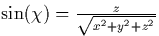 is the elevation angle of the point
is the elevation angle of the point  and
and  is the step
function. Equation (B.6) is a nonlinear equation for the field power
density since the non-Maxwellian nature of the distribution function under
an intense electric field (see latter the Fokker-Planck formalism) is
incorporated through
is the step
function. Equation (B.6) is a nonlinear equation for the field power
density since the non-Maxwellian nature of the distribution function under
an intense electric field (see latter the Fokker-Planck formalism) is
incorporated through 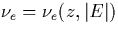 . The propagation of the fields
through the lower ionosphere is computed including the loss due to
self-absorption. This is how the field changes the properties of the medium.
We will assume that the field power density is below the ionization
threshold so that we don't have to estimate the time spatio-temporal
dependence of the electron density.
. The propagation of the fields
through the lower ionosphere is computed including the loss due to
self-absorption. This is how the field changes the properties of the medium.
We will assume that the field power density is below the ionization
threshold so that we don't have to estimate the time spatio-temporal
dependence of the electron density.
The plasma distribution function in the presence of an electric field is
strongly non-Maxwellian, therefore, a kinetic treatment to compute the
electron distribution function must be used. The kinetic treatment will be
necessary to find the relevant parameters for the field propagation, such as
the averaged total electron-neutral collisional frequency 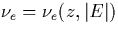 , or for the optical emissions, such as the excitation rates of
the different electronic levels. We use an existing Fokker-Planck code,
which has been developed for the description of ionospheric RF breakdown [Short et al. , 1990; Tsang et al., 1991; Papadopoulos et al., 1993a], and later used for studying such phenomena as
a triggered atmospheric breakdown [ Papadopoulos et al., 1993b],
and remote photometry of the atmosphere [ Papadopoulos et al.,
1994]. The code includes electron energization by collisional absorption of
the EM power in the presence of inelastic losses due to molecular N2 and
O 2. It has been an invaluable tool in producing a fully kinetic
description of ionospheric EM breakdown and has been successfully
benchmarked against the experimental data. The Fokker-Planck formalism [Gurevich 1978] starts by taking the spatially homogeneous Boltzmann
equation
, or for the optical emissions, such as the excitation rates of
the different electronic levels. We use an existing Fokker-Planck code,
which has been developed for the description of ionospheric RF breakdown [Short et al. , 1990; Tsang et al., 1991; Papadopoulos et al., 1993a], and later used for studying such phenomena as
a triggered atmospheric breakdown [ Papadopoulos et al., 1993b],
and remote photometry of the atmosphere [ Papadopoulos et al.,
1994]. The code includes electron energization by collisional absorption of
the EM power in the presence of inelastic losses due to molecular N2 and
O 2. It has been an invaluable tool in producing a fully kinetic
description of ionospheric EM breakdown and has been successfully
benchmarked against the experimental data. The Fokker-Planck formalism [Gurevich 1978] starts by taking the spatially homogeneous Boltzmann
equation
| 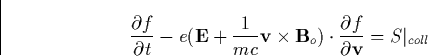 |
(35) |
For a weekly ionized plasma the distribution of electrons is mainly governed
by the interaction with neutrals, therefore, the electron-neutral
collisional term
| 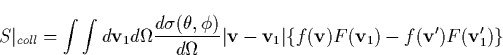 |
(36) |
include all the elastic and inelastic losses due to collisions with the
neutrals. In this collision integral, 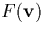 is the distribution
function of the neutrals in the atmosphere, v
is the distribution
function of the neutrals in the atmosphere, v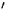 and v are the
velocity of the electron before and after the collision, v
and v are the
velocity of the electron before and after the collision, v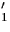 and
v1 are the velocity of the neutral before and after the collision. The
Scattering cross-section
and
v1 are the velocity of the neutral before and after the collision. The
Scattering cross-section 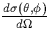 relates
the angles between the initial v
relates
the angles between the initial v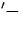 v
v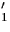 and final v-v1 relative velocities. In the presence of an electric field, we expand the
Boltzmann equation in terms of directional terms [Gurevich 1978]
and final v-v1 relative velocities. In the presence of an electric field, we expand the
Boltzmann equation in terms of directional terms [Gurevich 1978]
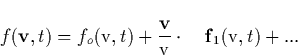
By taking the zeroth and first velocity moments, i.e. integrate the angular
variables over the shell 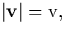 of the resulting
equation we obtain
of the resulting
equation we obtain
| 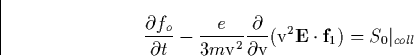 |
(37) |
| 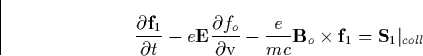 |
(38) |
where 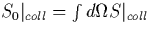 and
and 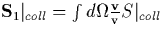 are the collisional
integrals respectively.
are the collisional
integrals respectively.
Since for weakly ionized plasmas the first moment of the collisional
integral will converge faster than the zeroth moment [Huang, 1987],
we expect that 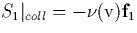 , which is usually
the closure scheme for expansion series of the above form. Such form for the
first moment of the collisional integral is also suggested by the fact that
the electron speed is larger than the neutral speed. The velocity dependent
effective collisional frequency
, which is usually
the closure scheme for expansion series of the above form. Such form for the
first moment of the collisional integral is also suggested by the fact that
the electron speed is larger than the neutral speed. The velocity dependent
effective collisional frequency 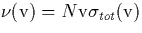 includes both elastic and inelastic processes, and
includes both elastic and inelastic processes, and 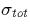 is the effective transport cross section. The elastic contribution
to the collisional integral gives [Gurevich 1978]
is the effective transport cross section. The elastic contribution
to the collisional integral gives [Gurevich 1978]
| ![\begin{displaymath}
S_0^e\vert _{coll}=\frac 1{2\mathrm{v}^2}\frac \partial {\pa...
...{kT}m\frac{\partial f_o}{\partial
\mathrm{v}}+\mathrm{v}f_o]\}\end{displaymath}](img609.gif) |
(39) |
where T is the temperature of the neutrals, and 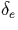 is the fraction
of the electron energy lost in an inelastic collision. The total inelastic
collision term is written as a sum of the following processes: rotational,
vibrational, optical, dissociation, attachment (including dissociative and
three-particle process), and ionization
is the fraction
of the electron energy lost in an inelastic collision. The total inelastic
collision term is written as a sum of the following processes: rotational,
vibrational, optical, dissociation, attachment (including dissociative and
three-particle process), and ionization
S0i|coll=Lrot+Lvib+Lopt+Ldis+Latt+Lion
We use Eq.(B.8) adapted for discrete energy transitions to obtain
the vibrational, dissociation and optical loses written as
![\begin{displaymath}
L=L_{vib}+L_{opt}+L_{dis}+L_{rot}=-\frac 2{m\mathrm{v}}\sum_...
...epsilon _{kj})-\epsilon f_o(\epsilon )\sigma _{kj}(\epsilon )] \end{displaymath}](img611.gif)
representing loss due to a transition (excitations and de-excitations) from
the state 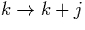 and a gain due to a transition that ends with
an electron energy
and a gain due to a transition that ends with
an electron energy 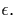 The
The 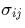 are the total cross
sections for the respective processes.
are the total cross
sections for the respective processes.
The attachment loss term is
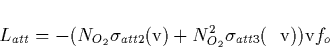
which includes dissociative attachment (1st term) along with triple
attachment (2nd term).
The losses due to ionization are given by
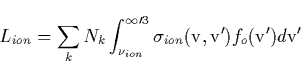
with v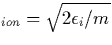 and
and 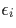 the ionization
energy. In this case the solution to Eq. (B.10) is
the ionization
energy. In this case the solution to Eq. (B.10) is 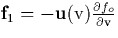 with
with 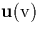 , the directed electron velocity, satisfying
, the directed electron velocity, satisfying
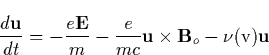
and the solution is given by Eq.(B.5), from which we derive that
![\begin{displaymath}
\mathbf{u}\cdot \mathbf{E}=\frac{eE_o^2\nu }{m[\Omega _B^2+\nu ^2]}\{1+\frac{
\Omega _B^2}{\nu ^2}\cos ^2\theta _o\} \end{displaymath}](img622.gif)
Therefore, the Fokker-Planck equation for the oscillating electric field is
given by
| 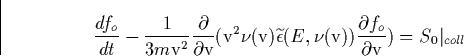 |
(40) |
where ![$\widetilde{\epsilon }(E,\nu )=\frac{e^2E_o^2}{2m[\Omega _B^2+\nu ^2]}
\{1+(\frac{\Omega _B}\nu )^2\cos ^2\theta _o\}$](img624.gif) is the quiver energy that
depends nonlinearly on the collisional frequency
is the quiver energy that
depends nonlinearly on the collisional frequency 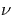 , the field Eo and
the height h in the atmosphere. The averaged electron-neutral collisional
frequency over the resulting distribution function is then denoted by
, the field Eo and
the height h in the atmosphere. The averaged electron-neutral collisional
frequency over the resulting distribution function is then denoted by 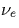 .
.
The Fokker-Planck equation, given by Eq.(B.12), is solved
numerically. The major assumption involved in the derivation of Eq.(B.12) are:
- The plasma is locally uniform, and spatial diffusion operates on much
longer time scales than the time it takes for the distribution function to
reach a steady state, so transport may be neglected
- The fractional ionization is low, so electron-electron and
electron-ion elastic collisions, as well as detachment and recombination,
may be ignored.
- The number of molecules in excited states is low, so superelastic
collisions are unimportant.
We must now relate the results from Eq.(B.12) to the spatio-temporal
field. The spatial variable does not affect the model since transport has
been neglected, and the field is below the ionization threshold. Some
relevant issues to notice:
- Since
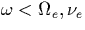 , the Fokker-Planck equation does not
depend on the frequency
, the Fokker-Planck equation does not
depend on the frequency 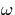 of the field.
of the field.
- In the absence of a field, the distribution function relaxes in a
time
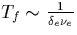 as can be inferred from Eq. (B.11). If
as can be inferred from Eq. (B.11). If 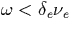 then the distribution function very
quickly reaches a steady state in the presence of the slowly varying field Eo2=E2(x,t). On the other extreme, if
then the distribution function very
quickly reaches a steady state in the presence of the slowly varying field Eo2=E2(x,t). On the other extreme, if 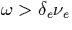 then the
field is too fast for the electrons to catch up and the distribution
function also settles in a steady state in the presence of the field for
which
then the
field is too fast for the electrons to catch up and the distribution
function also settles in a steady state in the presence of the field for
which 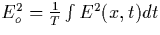 , i.e. the time envelope of the mean
root square of the field. Hence, we expect that the distribution function
will reach a steady state very quickly. In fact, we checked that for the
heights of interest, the distribution function did reach a steady state in a
time scale
, i.e. the time envelope of the mean
root square of the field. Hence, we expect that the distribution function
will reach a steady state very quickly. In fact, we checked that for the
heights of interest, the distribution function did reach a steady state in a
time scale 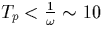
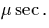 Therefore, we can take
the input field Eo2 to the Fokker-Planck equation to be the
instantaneous field E2(x,t).
Therefore, we can take
the input field Eo2 to the Fokker-Planck equation to be the
instantaneous field E2(x,t).
- The type of electron distribution function generated are highly
non-Maxwellian and can be found in Tsang et al. [1991]. There are
two ways of examining the results of Eq. (B.12). The solutions to
Eq. (B.12 ) can be parametrized in two ways. We can specify the
altitude h and the electric field amplitude Eo2. The alternative is to
find the collision frequency
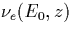 explicitly from the
Fokker-Planck code, and proceed with the self-similar solution for f(v) as a
function of
explicitly from the
Fokker-Planck code, and proceed with the self-similar solution for f(v) as a
function of 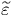 . Under the steady state regime, the
quiver energy
. Under the steady state regime, the
quiver energy 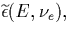 with
with 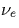 as the
averaged electron-neutral collisional frequency, serves as an excellent
parametrization of the steady state distribution function. The quiver energy
as the
averaged electron-neutral collisional frequency, serves as an excellent
parametrization of the steady state distribution function. The quiver energy
![$\widetilde{\epsilon }=\frac{e^2E^2(h)}{2m[\Omega _B^2+\nu _e^2(\widetilde{\epsilon })]}\{1+(\frac{\Omega _B}{\nu _e(\widetilde{\epsilon })})^2\cos
^2\theta _o\}$](img635.gif) becomes an implicit function of the height and the field
strength [Papadopoulos et al., 1993a].
becomes an implicit function of the height and the field
strength [Papadopoulos et al., 1993a].
- In the equations for
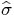 and
and 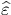 , we use the value
, we use the value 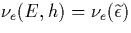 .
.
All of the above assumptions are well satisfied for the electric field
intensities expected. In addition, in the implementation of the numerical
solution, the neutral atmosphere is assumed to consist of molecular oxygen
and nitrogen only, excluding trace neutral constituents. Finally, using the
Fokker-Planck code with the electric field distribution from the fractal
antenna including the absorption, the intensities of the spatio-temporal
optical emissions will be obtained.
Consider the excitation of the 1st positive (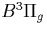 ) level of molecular
nitrogen N2 which has an excitation energy of 7.35 eV, and a lifetime of
8
) level of molecular
nitrogen N2 which has an excitation energy of 7.35 eV, and a lifetime of
8 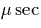 . The emission from the 1st positive band is predominantly in
the red. The other relevant line in the red part of the spectrum is the
. The emission from the 1st positive band is predominantly in
the red. The other relevant line in the red part of the spectrum is the 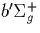 of molecular oxygen O2 which has an excitation
energy of 1.63 eV, but a very long lifetime of 12
of molecular oxygen O2 which has an excitation
energy of 1.63 eV, but a very long lifetime of 12 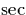 , and it is
collisionally quenched at the relevant heights. We can compute the
excitation rate of the 1st positive of N2 from the Fokker-Planck code for
a given field power density
, and it is
collisionally quenched at the relevant heights. We can compute the
excitation rate of the 1st positive of N2 from the Fokker-Planck code for
a given field power density
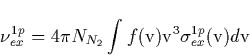
where 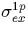 is the excitation cross-section. Under a steady
state situation, which is consistent with the lifetime
is the excitation cross-section. Under a steady
state situation, which is consistent with the lifetime 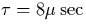 of
this N2(1P), the excitations are then followed by optical emissions where
the number of photons emitted per sec, per cm3 is given by
of
this N2(1P), the excitations are then followed by optical emissions where
the number of photons emitted per sec, per cm3 is given by 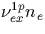 for an given electron density ne. In order to compare with
observations, we will need to average the number of photons in this band at
a given position in space over a time
for an given electron density ne. In order to compare with
observations, we will need to average the number of photons in this band at
a given position in space over a time 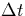 . Hence
. Hence
![\begin{displaymath}
<\nu _{ex}^{1p}n_e\gt=\frac 1{\Delta t}\int_0^{\Delta t}\nu
_{ex}^{1p}[E(t)]n_edt \end{displaymath}](img644.gif)
The intensity of the radiative transition in Rayleighs is then given by
| 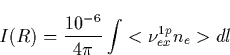 |
(41) |
where the integral is carried along the visual path of the detector (column
integrated). Therefore, a Rayleigh (R) is the number of photons per sec per
cm2 column integrated and normalized to 106 photons.
Figure B.1:
(a) The two electrond density profiles as a function of heigh. (c)
The absoption of the E field is followed by optical emissions of the N2
(1P). (d) The exitation rates. Plots correspond to the tenous night-time ne(1) electron density profile (dotted line) and dense night-time ne(2) electron density profile (dashed line).
![\begin{figure}
\center
\includegraphics [width=6in,height=4in]{images/dipole.eps}\end{figure}](img646.gif) |
Consider first the field due to a point radiator, i.e. 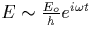 , we can then compute the field propagation including
self-absorption, as shown in Fig B.1b, for the two electron density
n e profiles shown in Fig. B.1a, typical tenuous and dense
electron density profiles respectively. Similarly, we can compute the
optical emission intensity for the two profiles as shown in Fig. B.1
c. The excitations rates of N2(1P) for the different altitudes is given
in Fig. B.1d as a function of the power density S(W/m2)=c
, we can then compute the field propagation including
self-absorption, as shown in Fig B.1b, for the two electron density
n e profiles shown in Fig. B.1a, typical tenuous and dense
electron density profiles respectively. Similarly, we can compute the
optical emission intensity for the two profiles as shown in Fig. B.1
c. The excitations rates of N2(1P) for the different altitudes is given
in Fig. B.1d as a function of the power density S(W/m2)=c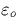 E2(V/m).
E2(V/m).
From now on we take the tenuous electron density profile ne=ne(1). We
can compute the height dependent field propagation and photon emissions
using this simple monopole model for different electric power density
profiles starting at the height h=60 km. Figure B.2 shows the
field propagation and emissions for different field strengths propagating
from h=60 km. It gives us an idea of the electric field power intensity
required to produce observable emissions.
Figure B.2:
(a) The field propagation for the point dipole model as a function
of height for different power densitties hitting h=60 km. (b) The emissions
produced by the fields shown in part (a). The three curves correspond to
different field power densities at h=60 km as seen in Fig. B.2.
![\begin{figure}
\center
\includegraphics [width=5in,height=4in]{images/fe.eps}\end{figure}](img649.gif) |
As we commented above, the quiver energy 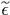 can
parametrize the steady state distribution function. As we increase the power
density S(W/m2), we will reach a threshold value of
can
parametrize the steady state distribution function. As we increase the power
density S(W/m2), we will reach a threshold value of 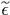 where the electrons will gain enough energy to induce significant
ionization. This threshold value occurs at
where the electrons will gain enough energy to induce significant
ionization. This threshold value occurs at ![$\widetilde{\epsilon }
(eV)=1.7\,(2\pi \times 10^6)^2\frac{\mathrm{E}^2(V/m)}{[\Omega _B^2+\nu
_e^2] }\{1+(\frac{\Omega _B}{\nu _e})^2\cos ^2\theta _o\}\sim 0.1$](img651.gif) eV [
Papadopoulos et al., 1993a] which can be computed at a given
height and electric power density.
eV [
Papadopoulos et al., 1993a] which can be computed at a given
height and electric power density.
Taking 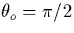 , we can estimate the power density required at
h=60 km, from our point radiator model, to produce ionization at some height
above 60 km. Of course ionization will not occur at h=60 km for these power
densities, but assuming the propagation shown in Fig. B.2 we can
estimate whether ionization will occur at a higher height for a given field
strength at h=60 km. Figure B.3 shows the quiver energy height
profile for the field profiles shown in Fig. B.2. Therefore, the
ionization threshold will be reached at some height (
, we can estimate the power density required at
h=60 km, from our point radiator model, to produce ionization at some height
above 60 km. Of course ionization will not occur at h=60 km for these power
densities, but assuming the propagation shown in Fig. B.2 we can
estimate whether ionization will occur at a higher height for a given field
strength at h=60 km. Figure B.3 shows the quiver energy height
profile for the field profiles shown in Fig. B.2. Therefore, the
ionization threshold will be reached at some height (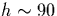 km) if
km) if 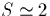 W/m2 at a height of h=60 km.
W/m2 at a height of h=60 km.
Figure B.3:
The quiver energy as a function of height for the field intensities
shown in Fig. B.2a. The three curves correspond to different field
power densities at h=60 km corresponding to Fig. B.2.
![\begin{figure}
\center
\includegraphics [width=5in,height=4in]{images/quiv.eps}\end{figure}](img654.gif) |
Next: Population of N2 Levels
Previous: Fields from a Fractal
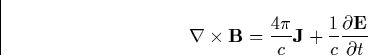
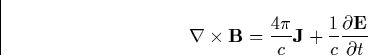

![]()
![]()
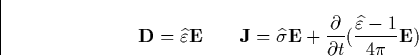
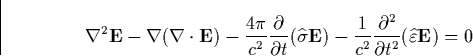
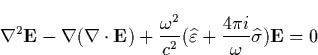
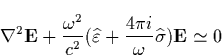
![\begin{displaymath}
\mathbf{E}(s,t)\simeq \frac{\mathbf{E}(0,t-\frac sc)}{s^2}\t...
..._{\mathbf{s}}[i\widehat{n}-\widehat{\Gamma }]\cdot d\mathbf{s}}\end{displaymath}](img560.gif)
![]()
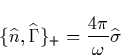
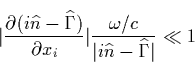
![]() and
and ![]() on the field E and the validity of
the independence of
on the field E and the validity of
the independence of ![]() and
and ![]() in
time. Again following [Gurevich 1978] we will estimate the
dependence of the
in
time. Again following [Gurevich 1978] we will estimate the
dependence of the ![]() and
and ![]() on the
field strength by looking at the plasma average velocity and energy. When
the field effects become important we will see later that the electron
distribution will have a strong directional component with the average
plasma velocity
on the
field strength by looking at the plasma average velocity and energy. When
the field effects become important we will see later that the electron
distribution will have a strong directional component with the average
plasma velocity ![]() given by
given by
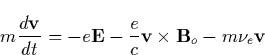
![\begin{displaymath}
\mathbf{v}_e=\frac{eE_o}{m[\Omega _B^2+(i\omega -\nu _e)^2]}...
...}}+\Omega _B(\widehat{\mathbf{e}}\times \widehat{\mathbf{b}})\}\end{displaymath}](img575.gif)
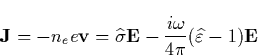
![]() and
and ![]() are not very illuminating, but we are interested in the case in which
are not very illuminating, but we are interested in the case in which ![]() under the influence of the field. Let's define
under the influence of the field. Let's define ![]() to be the angle between the magnetic field and the horizontal. In
this approximation the conductivity tensor is
to be the angle between the magnetic field and the horizontal. In
this approximation the conductivity tensor is
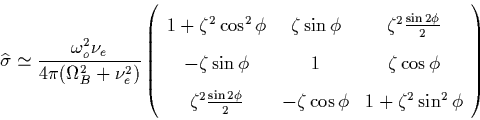
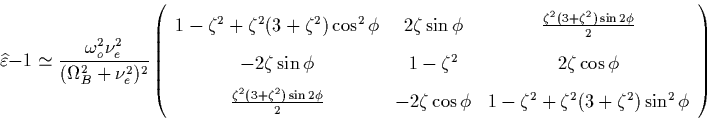
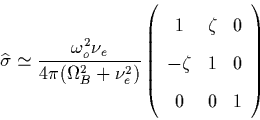
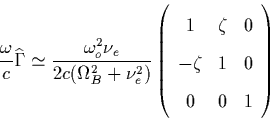
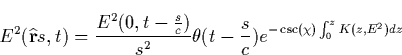
![]() , or for the optical emissions, such as the excitation rates of
the different electronic levels. We use an existing Fokker-Planck code,
which has been developed for the description of ionospheric RF breakdown [Short et al. , 1990; Tsang et al., 1991; Papadopoulos et al., 1993a], and later used for studying such phenomena as
a triggered atmospheric breakdown [ Papadopoulos et al., 1993b],
and remote photometry of the atmosphere [ Papadopoulos et al.,
1994]. The code includes electron energization by collisional absorption of
the EM power in the presence of inelastic losses due to molecular N2 and
O 2. It has been an invaluable tool in producing a fully kinetic
description of ionospheric EM breakdown and has been successfully
benchmarked against the experimental data. The Fokker-Planck formalism [Gurevich 1978] starts by taking the spatially homogeneous Boltzmann
equation
, or for the optical emissions, such as the excitation rates of
the different electronic levels. We use an existing Fokker-Planck code,
which has been developed for the description of ionospheric RF breakdown [Short et al. , 1990; Tsang et al., 1991; Papadopoulos et al., 1993a], and later used for studying such phenomena as
a triggered atmospheric breakdown [ Papadopoulos et al., 1993b],
and remote photometry of the atmosphere [ Papadopoulos et al.,
1994]. The code includes electron energization by collisional absorption of
the EM power in the presence of inelastic losses due to molecular N2 and
O 2. It has been an invaluable tool in producing a fully kinetic
description of ionospheric EM breakdown and has been successfully
benchmarked against the experimental data. The Fokker-Planck formalism [Gurevich 1978] starts by taking the spatially homogeneous Boltzmann
equation
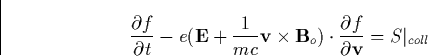
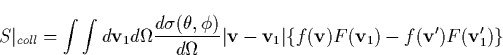
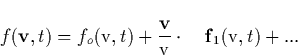
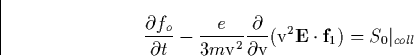
![]() , which is usually
the closure scheme for expansion series of the above form. Such form for the
first moment of the collisional integral is also suggested by the fact that
the electron speed is larger than the neutral speed. The velocity dependent
effective collisional frequency
, which is usually
the closure scheme for expansion series of the above form. Such form for the
first moment of the collisional integral is also suggested by the fact that
the electron speed is larger than the neutral speed. The velocity dependent
effective collisional frequency ![]() includes both elastic and inelastic processes, and
includes both elastic and inelastic processes, and ![]() is the effective transport cross section. The elastic contribution
to the collisional integral gives [Gurevich 1978]
is the effective transport cross section. The elastic contribution
to the collisional integral gives [Gurevich 1978]
![\begin{displaymath}
S_0^e\vert _{coll}=\frac 1{2\mathrm{v}^2}\frac \partial {\pa...
...{kT}m\frac{\partial f_o}{\partial
\mathrm{v}}+\mathrm{v}f_o]\}\end{displaymath}](img609.gif)
![\begin{displaymath}
L=L_{vib}+L_{opt}+L_{dis}+L_{rot}=-\frac 2{m\mathrm{v}}\sum_...
...epsilon _{kj})-\epsilon f_o(\epsilon )\sigma _{kj}(\epsilon )] \end{displaymath}](img611.gif)
![]()
![\begin{displaymath}
\mathbf{u}\cdot \mathbf{E}=\frac{eE_o^2\nu }{m[\Omega _B^2+\nu ^2]}\{1+\frac{
\Omega _B^2}{\nu ^2}\cos ^2\theta _o\} \end{displaymath}](img622.gif)
![]() ) level of molecular
nitrogen N2 which has an excitation energy of 7.35 eV, and a lifetime of
8
) level of molecular
nitrogen N2 which has an excitation energy of 7.35 eV, and a lifetime of
8 ![]() . The emission from the 1st positive band is predominantly in
the red. The other relevant line in the red part of the spectrum is the
. The emission from the 1st positive band is predominantly in
the red. The other relevant line in the red part of the spectrum is the ![]() of molecular oxygen O2 which has an excitation
energy of 1.63 eV, but a very long lifetime of 12
of molecular oxygen O2 which has an excitation
energy of 1.63 eV, but a very long lifetime of 12 ![]() , and it is
collisionally quenched at the relevant heights. We can compute the
excitation rate of the 1st positive of N2 from the Fokker-Planck code for
a given field power density
, and it is
collisionally quenched at the relevant heights. We can compute the
excitation rate of the 1st positive of N2 from the Fokker-Planck code for
a given field power density
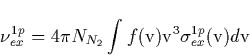
![\begin{displaymath}
<\nu _{ex}^{1p}n_e\gt=\frac 1{\Delta t}\int_0^{\Delta t}\nu
_{ex}^{1p}[E(t)]n_edt \end{displaymath}](img644.gif)
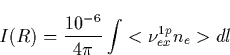
![\begin{figure}
\center
\includegraphics [width=6in,height=4in]{images/dipole.eps}\end{figure}](img646.gif)
![]() , we can then compute the field propagation including
self-absorption, as shown in Fig B.1b, for the two electron density
n e profiles shown in Fig. B.1a, typical tenuous and dense
electron density profiles respectively. Similarly, we can compute the
optical emission intensity for the two profiles as shown in Fig. B.1
c. The excitations rates of N2(1P) for the different altitudes is given
in Fig. B.1d as a function of the power density S(W/m2)=c
, we can then compute the field propagation including
self-absorption, as shown in Fig B.1b, for the two electron density
n e profiles shown in Fig. B.1a, typical tenuous and dense
electron density profiles respectively. Similarly, we can compute the
optical emission intensity for the two profiles as shown in Fig. B.1
c. The excitations rates of N2(1P) for the different altitudes is given
in Fig. B.1d as a function of the power density S(W/m2)=c![]() E2(V/m).
E2(V/m).
![\begin{figure}
\center
\includegraphics [width=5in,height=4in]{images/fe.eps}\end{figure}](img649.gif)
![]() can
parametrize the steady state distribution function. As we increase the power
density S(W/m2), we will reach a threshold value of
can
parametrize the steady state distribution function. As we increase the power
density S(W/m2), we will reach a threshold value of ![]() where the electrons will gain enough energy to induce significant
ionization. This threshold value occurs at
where the electrons will gain enough energy to induce significant
ionization. This threshold value occurs at ![]() eV [
Papadopoulos et al., 1993a] which can be computed at a given
height and electric power density.
eV [
Papadopoulos et al., 1993a] which can be computed at a given
height and electric power density.
![]() , we can estimate the power density required at
h=60 km, from our point radiator model, to produce ionization at some height
above 60 km. Of course ionization will not occur at h=60 km for these power
densities, but assuming the propagation shown in Fig. B.2 we can
estimate whether ionization will occur at a higher height for a given field
strength at h=60 km. Figure B.3 shows the quiver energy height
profile for the field profiles shown in Fig. B.2. Therefore, the
ionization threshold will be reached at some height (
, we can estimate the power density required at
h=60 km, from our point radiator model, to produce ionization at some height
above 60 km. Of course ionization will not occur at h=60 km for these power
densities, but assuming the propagation shown in Fig. B.2 we can
estimate whether ionization will occur at a higher height for a given field
strength at h=60 km. Figure B.3 shows the quiver energy height
profile for the field profiles shown in Fig. B.2. Therefore, the
ionization threshold will be reached at some height (![]() km) if
km) if ![]() W/m2 at a height of h=60 km.
W/m2 at a height of h=60 km.
![\begin{figure}
\center
\includegraphics [width=5in,height=4in]{images/quiv.eps}\end{figure}](img654.gif)