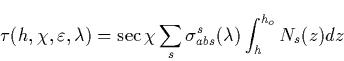![\begin{figure}
\center
\includegraphics [width=4in,height=4in]{images/n2levels.eps}\end{figure}](img655.gif) |
The electron energization is computed with the help of the Fokker-Planck code (described in Appendix B). For definiteness we assume that the emission region is located at z=80 km [Lyons , 1994; Sentman et al., 1995; Bossipio et al., 1995; Winckler et al., 1996].
![\begin{figure}
\center
\includegraphics [width=4in,height=4in]{images/n2levels.eps}\end{figure}](img655.gif) |
In the current model we have retained only the electronic levels of N2
shown in Fig. C.1. The computation of the intensity of a radiative
transition connecting the v-th and v![]() -th vibrational levels of
electronic states
-th vibrational levels of
electronic states ![]() and
and ![]() is accomplished as following. We
first compute the excitation rate
is accomplished as following. We
first compute the excitation rate ![]() of the
of the ![]() electronic level of N2 by electron impact
electronic level of N2 by electron impact
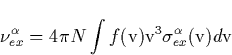
Figure C.2 shows the excitation rates for the relevant electronic
levels of N2 as a function of the electric field Eo at this height z=80 km. We have neglected effects caused by the W![]() B
transition compared with that due to the B
B
transition compared with that due to the B![]() transition, both having similar excitation threshold but different
excitation rates as revealed by Fig (C.2). We then obtain the
population of vibrational levels inside each of the electronic states by
solving the following set of stationary equations [Cartwright,
1978]
transition, both having similar excitation threshold but different
excitation rates as revealed by Fig (C.2). We then obtain the
population of vibrational levels inside each of the electronic states by
solving the following set of stationary equations [Cartwright,
1978]
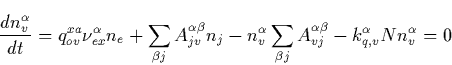 |
(42) |
Therefore, the first term in the right side of Eq. (C.1) shows the
direct pumping of the v vibrational level of the ![]() electronic state
by the electron impact. While the second term shows cascade excitation, the
third term describes the radiation losses. The last term reveals losses due
to the collisional quenching. Note that the usage of the stationary
equations for the population of vibrational level is justified by the fact
that radiative lifetime of the relevant electronic states have to be shorter
than the duration T of electromagnetic pulse from lightning in order to be
effectively pumped. Therefore, a stationary distribution of
electronic state
by the electron impact. While the second term shows cascade excitation, the
third term describes the radiation losses. The last term reveals losses due
to the collisional quenching. Note that the usage of the stationary
equations for the population of vibrational level is justified by the fact
that radiative lifetime of the relevant electronic states have to be shorter
than the duration T of electromagnetic pulse from lightning in order to be
effectively pumped. Therefore, a stationary distribution of ![]() is
established during the pulse.
is
established during the pulse.
From Eq. (C.1) we obtain now the population of the ![]() electronic level as
electronic level as
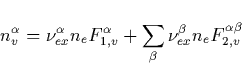
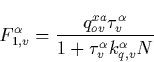
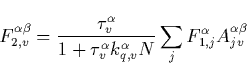 |
(43) |
Note that collisional transfer between the N2(B) and other excited N2
states could affect the N2 optical spectrum [Morill and Benesh,
1996] and is an important issue for quasistationary auroras. However, in
order to affect sprite spectra, the collisions has to occur faster than the
duration of a sprite, T![]() m
m![]() , which requires that the density
of the excited nitrogen molecules to be larger than
, which requires that the density
of the excited nitrogen molecules to be larger than ![]() cm-3. (Here the collision rate coefficient is
assumed to be
cm-3. (Here the collision rate coefficient is
assumed to be ![]() cm3s-1 [Morill
and Benesh 1996]). To produce such significant abundance of the
electronically excited molecules about 109 J km-3 has to be
released. Such value limits the application of the above effect to some
local spots, since the total energy released when a charge of hundreds of
Coulombs is transferred from cloud to ground is about 1011 J [ Uman , 1987], and only a small fraction of this energy is absorbed in the
ionosphere producing the red sprite.
cm3s-1 [Morill
and Benesh 1996]). To produce such significant abundance of the
electronically excited molecules about 109 J km-3 has to be
released. Such value limits the application of the above effect to some
local spots, since the total energy released when a charge of hundreds of
Coulombs is transferred from cloud to ground is about 1011 J [ Uman , 1987], and only a small fraction of this energy is absorbed in the
ionosphere producing the red sprite.
The intensity of the radiative transition in Rayleighs connecting the v-th
and v![]() -th vibrational levels of electronic states
-th vibrational levels of electronic states ![]() and
and ![]() by
by
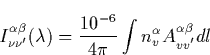 |
(44) |
The observed spectrum depends on the location of the detector. If observed
from space, the spectrum is the same as the source spectrum ![]() , while if observed from either ground or airplane it will be distorted by
atmospheric attenuation. Atmospheric attenuation depends on the zenith angle
, while if observed from either ground or airplane it will be distorted by
atmospheric attenuation. Atmospheric attenuation depends on the zenith angle
![]() of the optical source, the altitude ho of the detector, and on
the properties of the atmosphere, such as relative humidity and aerosol
density. We consider the following contributions to the attenuation:
absorption by ozone, oxygen and water vapor, the Rayleigh scattering by air
molecule, and Mie scattering by aerosols. The total attenuation of the
optical emission is the result of the above contributions and is given by
of the optical source, the altitude ho of the detector, and on
the properties of the atmosphere, such as relative humidity and aerosol
density. We consider the following contributions to the attenuation:
absorption by ozone, oxygen and water vapor, the Rayleigh scattering by air
molecule, and Mie scattering by aerosols. The total attenuation of the
optical emission is the result of the above contributions and is given by
| |
(45) |