We proceed next to model the spectrum of red sprites due to the electron
energization by the electric field from lightning. It capitalizes on the
fact that there are two distinct timescales. A fast timescale on which a
steady state electron distribution function ![]() is established
by balancing the electron energization rate with inelastic loses (see
Appendix B), and a slow radiation timescale dominated by interlevel transfer
and collisional quenching.
is established
by balancing the electron energization rate with inelastic loses (see
Appendix B), and a slow radiation timescale dominated by interlevel transfer
and collisional quenching.
The electron energization is computed with the help of the Fokker-Planck code (described in Appendix B). We assume first that sprites located at a certain height z, and for the sake of definiteness assume that z=80 km [Lyons , 1994; Sentman et al., 1995; Bossipio et al., 1995; Winckler et al., 1996]. Then we discuss a more realistic model of a spatially integrated spectrum of red sprites.
Radiative deexcitation of the excited molecules produces optical flashes that superficially resemble those observed during auroras. However, unlike auroras which last for hours and in which even forbidden transitions need to be considered, red sprites have millisecond duration, so that only N2 transitions faster than a millisecond excited by direct electron impact or through cascades need to be retained (Fig. C.1). The radiative deexcitation involves:
The usage of the stationary equations for the population of vibrational
level is justified by the fact that radiative lifetime of the relevant
electronic states have to be shorter than the duration T of electromagnetic
pulse from lightning in order to be effectively pumped. Therefore, a
stationary distribution of ![]() is established during the pulse.
is established during the pulse.
Note that since we consider the shape of sprite spectrum, only relative line
intensities are of interest. Furthermore, the vibrational-electronic
population depends linearly on the electron density (see Eq. (C.2));
as a result the spectrum is not affected by the possible increase in the
electron density due to the ionization of the neutral gas by ''hot''
electrons. Using the above computational scheme we find the synthetic source
spectrum ![]() of N2 localized at 80 km which includes the
first and second positive and first negative bands. It is presented in Fig.
4.1 for two values of the electric field amplitude E0= 35 and 70
V/m. Notice that only the 1P and 2P bands give a distinctive contribution to
the source spectrum, while the N2+(1N) band plays only a minor role
since it can only be excited by ''tail'' electron having energy in excess of
19 eV. In comparison, this N2+(1N) band is among the brightest in
auroras since it is caused by high energy electrons.
of N2 localized at 80 km which includes the
first and second positive and first negative bands. It is presented in Fig.
4.1 for two values of the electric field amplitude E0= 35 and 70
V/m. Notice that only the 1P and 2P bands give a distinctive contribution to
the source spectrum, while the N2+(1N) band plays only a minor role
since it can only be excited by ''tail'' electron having energy in excess of
19 eV. In comparison, this N2+(1N) band is among the brightest in
auroras since it is caused by high energy electrons.
![\begin{figure}
\center
\includegraphics [width=4in]{images/sourcespec.eps}\end{figure}](img244.gif) |
The observed spectrum depends on the location of the detector. If observed
from space, the spectrum is the same as the source spectrum ![]() , while if observed from either ground or airplane it will be distorted by
atmospheric attenuation. Atmospheric attenuation depends on the zenith angle
, while if observed from either ground or airplane it will be distorted by
atmospheric attenuation. Atmospheric attenuation depends on the zenith angle
![]() of the optical source, the altitude ho of the detector, and on
the properties of the atmosphere, such as relative humidity and aerosol
density. We consider the following contributions to the attenuation:
of the optical source, the altitude ho of the detector, and on
the properties of the atmosphere, such as relative humidity and aerosol
density. We consider the following contributions to the attenuation:
Figure 4.2 reveals the model sprite spectrum as observed by a ground
based detector viewing the source at zero zenith angle ![]() . This
spectrum differs significantly from the synthetic source spectrum 4.1
. First, the N2(2P) and N2+(1N) bands are attenuated more
significantly than the N2(1P) band. This effect is stronger for longer
optical paths corresponding to higher zenith angle as seen in Fig 4.3
. By comparing the two peaks of the N2(1P) band, say 5-2 and 4-2 which
undergo different absorption, one can estimate the zenith angle of the
observed sprite.
. This
spectrum differs significantly from the synthetic source spectrum 4.1
. First, the N2(2P) and N2+(1N) bands are attenuated more
significantly than the N2(1P) band. This effect is stronger for longer
optical paths corresponding to higher zenith angle as seen in Fig 4.3
. By comparing the two peaks of the N2(1P) band, say 5-2 and 4-2 which
undergo different absorption, one can estimate the zenith angle of the
observed sprite.
From the optical spectrum one can retrieve the intensity of the pumping electric field. This is accomplished by comparing lines either belonging to different bands or to the same band. In the first case the ratio of excitation rates of the corresponding electronic levels depends on the direct pumping of the levels (mainly) and from cascades excitation. In the second case this ratio is controlled by the cascades excitation only.
Since only a few lines belonging to the 1P band have been observed so far [
Mende et al., 1995; Hampton et al., 1996], in what follows
we consider the vibrational transitions v - v![]() and v1-v
and v1-v![]() belonging to the N2(1P) band. For given values of the
relative intensities of two chosen spectral lines
belonging to the N2(1P) band. For given values of the
relative intensities of two chosen spectral lines ![]() and
and ![]() we obtain using Eqs. (C.2), (C.3) that
we obtain using Eqs. (C.2), (C.3) that
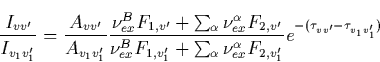 |
(10) |
Generally speaking, one can obtain ratios ![]() ,
, ![]() and
and ![]() by using
intensities of three different spectral bands. This allows the evaluation of
the electric field amplitude from Fig. C.2. This procedure requires
knowledge of the atmospheric attenuation, which includes the zenith angle,
as well as the relative humidity, and the aerosol number density. However,
if the detector is boarded on a high altitude airplane, the absorption
caused by the water vapor and aerosols becomes negligible. Thus the
retrieval procedure is simplified. In order to illustrate the opportunities
given by the proposed method we consider data from Hampton et al.
[1996] presented in Fig. 4.4a which only shows the N2(1P) band.
The ratio of the intensities of the 6-3 to the 7-4 transitions is 0.62/0.4.
We take into account that for the chosen transitions the largest role is
played by the direct pumping of the B level and by the cascade from the B
by using
intensities of three different spectral bands. This allows the evaluation of
the electric field amplitude from Fig. C.2. This procedure requires
knowledge of the atmospheric attenuation, which includes the zenith angle,
as well as the relative humidity, and the aerosol number density. However,
if the detector is boarded on a high altitude airplane, the absorption
caused by the water vapor and aerosols becomes negligible. Thus the
retrieval procedure is simplified. In order to illustrate the opportunities
given by the proposed method we consider data from Hampton et al.
[1996] presented in Fig. 4.4a which only shows the N2(1P) band.
The ratio of the intensities of the 6-3 to the 7-4 transitions is 0.62/0.4.
We take into account that for the chosen transitions the largest role is
played by the direct pumping of the B level and by the cascade from the B![]() level. The difference in the atmospheric attenuations, as we
check with our model, was less than a few percent for the zenith angle
level. The difference in the atmospheric attenuations, as we
check with our model, was less than a few percent for the zenith angle ![]() . Substituting into Eq. (4.1) the ratio of the intensities
we obtain that
. Substituting into Eq. (4.1) the ratio of the intensities
we obtain that ![]() , and
according to Fig. C.2 this corresponds to the electric field
amplitude Eo=35 V/m which at z=80 km is below the breakdown
threshold. Note that this estimate was made using noisy data which are not
spatially resolved, and can be considered only as an illustrative example.
However, the synthetic spectrum calculated for the electric field amplitude
E o=35 V/m, the zenith angle of
, and
according to Fig. C.2 this corresponds to the electric field
amplitude Eo=35 V/m which at z=80 km is below the breakdown
threshold. Note that this estimate was made using noisy data which are not
spatially resolved, and can be considered only as an illustrative example.
However, the synthetic spectrum calculated for the electric field amplitude
E o=35 V/m, the zenith angle of ![]() 80o, and for the detector
location of 4.3 km above the sea level, which is shown in Fig. 4.4b,
resembles that observed by Hampton et al. [1996] at similar
conditions, as revealed by Fig. 4.4a.
80o, and for the detector
location of 4.3 km above the sea level, which is shown in Fig. 4.4b,
resembles that observed by Hampton et al. [1996] at similar
conditions, as revealed by Fig. 4.4a.
![\begin{figure}
\center
\includegraphics [width=5.5in,height=4in]{images/spec-comp.1.eps}\end{figure}](img261.gif) |
To compare with actual spectrum measurements, we must consider the detector column integration, as photons are emitted from different heights under different conditions, e.g. quiver energies, electron densities, neutral densities, collisional quenching, etc. The column integration, Eq. ( C.3), must be carried carefully due to two factors:
We can apply the method we explained above to the electric field produced by
our fractal lightning model in the lower ionosphere, as discussed in Chapter
2 and 3. For a definiteness we assume that the lightning discharge has a
fractal dimension D=1.2 (![]() with a current peak of Io=100 kA.
We chose the field profile at the core of the sprites to carry the spatial
integration Eq. (C.3). The result is shown in Fig. 4.5. In
fact, for this electric field profile, the relative spectrum does not change
considerably from the, properly normalized, spectrum computed for a slab at h=80 km and of
with a current peak of Io=100 kA.
We chose the field profile at the core of the sprites to carry the spatial
integration Eq. (C.3). The result is shown in Fig. 4.5. In
fact, for this electric field profile, the relative spectrum does not change
considerably from the, properly normalized, spectrum computed for a slab at h=80 km and of ![]() eV (35 V/m) revealed by a dashed
line, the difference being only 10% for the short wavelengths of the 2P
band and less than 1% for the longer wavelengths of the 1P band. We
expected that the differences become more pronounce as the sprites spread
downward below 70 km.
eV (35 V/m) revealed by a dashed
line, the difference being only 10% for the short wavelengths of the 2P
band and less than 1% for the longer wavelengths of the 1P band. We
expected that the differences become more pronounce as the sprites spread
downward below 70 km.
In conclusion, a model of the red sprite spectrum due to molecular excitation by ionospheric electrons accelerated by the electric field from lightning was developed. The model could allow us to evaluate the electric field amplitude by comparing the intensities of different spectral lines. The model also reveals some differences between the aurora and sprite spectra: in the aurora both permitted and forbidden transitions play a noticeable role, while in sprites only permitted transitions are important. It seems that sprites are produced by electrons of much lesser energy than that of auroral electrons. Unlike the aurora, the collisions between excited molecules could affect sprites only in a few local spots. Sprites are normally observed at high zenith angle, so the spectrum is highly influenced by the atmospheric attenuation. For a given zenith angle and atmospheric constitution (i.e. humidity and aerosol density), the collisional quenching and the atmospheric attenuation can be computed accurately. As a result, if the measurements have good spatial resolution, the model output could in principle yield the spatial profile of the amplitude of the electric field causing the sprite.
![\begin{figure}
\center
\includegraphics [width=3in,height=3in]{images/spec_spatial.eps}\end{figure}](img265.gif) |