![\begin{figure}
\center
\includegraphics [width=4in]{images/tasks.eps}\end{figure}](img216.gif) |
We now combine the ideas developed in the previous chapters and apply them to the modeling of red sprites. We have seen that the radiation pattern and intensity is critically dependent on the fractal model, e.g. the fractal dimension of the discharge. Therefore, we expect that the lightning parameters required to produce the red sprites are critically dependent on the discharge fractal dimension as well. We will study the current threshold required to produce the sprite for different fractal dimensions.
The modeling of the effects of the fractal lightning discharge on the lower ionosphere involves a series of steps, as it is shown in Fig. 3.1:
Therefore, the main parameters controlling the model are:
![\begin{figure}
\center
\includegraphics [width=4in]{images/tasks.eps}\end{figure}](img216.gif) |
The spatial geometry is defined with z as the height from the ground and x-y as the constant height cross-section. The horizontal fractal lightning discharge is constructed in the x-y plane at a height of zo=5 km from the ground (with the image discharge at zo=-5 km). The point x=0 km and y=0 km corresponds to the center of the discharge.
The stochastic fractal model is specially suitable for understanding the
dependence on the dimension of the discharge, since ![]() can be easily
parametrized as is plotted in Fig. 2.16. The spatio-temporal emission
pattern from the fractal discharge model can now be computed from the field
pattern that includes self-absorption. As an example, we take a discharge
current of
can be easily
parametrized as is plotted in Fig. 2.16. The spatio-temporal emission
pattern from the fractal discharge model can now be computed from the field
pattern that includes self-absorption. As an example, we take a discharge
current of ![]() kA and
kA and ![]() . Since the decay time
is
. Since the decay time
is ![]() s-1, the total amount of charge discharged is Q=200
C. The statistical relevance of such values for lightning and the
generation of sprites will be discussed latter.
s-1, the total amount of charge discharged is Q=200
C. The statistical relevance of such values for lightning and the
generation of sprites will be discussed latter.
For this case the field is below the ionization threshold in the lower ionosphere. For intensities exceeding the ionization threshold, the time evolution of the electron density must be included.
![\begin{figure}
\center
\includegraphics [width=6in,height=3in]{images/emi_t_3.0.eps}\end{figure}](img220.gif) |
The fractal dimension for the lightning discharge is ![]() . The
instantaneous field amplitude at z=85 km and x=0 km, including
self-absorption, is shown in Fig. 3.2a and the instantaneous optical
emission of the N2(1P) in Fig. 3.2b.
. The
instantaneous field amplitude at z=85 km and x=0 km, including
self-absorption, is shown in Fig. 3.2a and the instantaneous optical
emission of the N2(1P) in Fig. 3.2b.
![\begin{figure}
\center
\includegraphics [width=5in,height=4in]{images/emi_3.0_space.eps}\end{figure}](img222.gif) |
To compare the results with the sprite observations, we must average the photon flux over the time scale of sprites. The averaged number of photons per sec per cm3 can now be calculated as
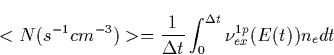 |
(9) |
![\begin{figure}
\center
\includegraphics [width=5in,height=3in]{images/emi_h_3.0.eps}\end{figure}](img225.gif) |
Of course, this value is computed locally at a single point, and we must repeat this procedure in space to deduce the spatial dependence of the emissions. The time averaged emission pattern from the lower ionosphere, for the horizontal cross-section along the line y=10 km, is shown in Fig. 3.3 for the discharge current of Io=200 kA. The color coding represents the number of photons emitted per sec per cc in dBs normalized by its average over the image region. The maximum intensity is about 100 kR for column integration along the x axis. We did check that the field intensities at all times were below the ionization threshold for this current of Io=200 kA. The fractal nature of the discharge can in fact produce a non-uniform emission pattern.
A plot of the number of emitted photons in units of kR/km as a function of
the discharge current Io is shown in Fig. 3.4 for the position at
the core of the sprite, i.e. as given for Fig.3.2. If the field
becomes larger than the ionization threshold, we must incorporate the time
evolution of the electron density. The ionization threshold is reached when ![]() eV which for our fractal model with the
propagation speed
eV which for our fractal model with the
propagation speed ![]() occurs at a critical current
occurs at a critical current ![]() kA. Since the power density scales as
kA. Since the power density scales as ![]() , we can
use Fig.3.4 as a reference for the requirements of the lightning
parameters to generate the sprite. Hence, for a faster discharge a sprite
can be produced with a lower current amplitude.
, we can
use Fig.3.4 as a reference for the requirements of the lightning
parameters to generate the sprite. Hence, for a faster discharge a sprite
can be produced with a lower current amplitude.
We proceed next to determine the spatial structure of the optical emissions
as a function of the dimension D. We consider the 4 fractal discharges ![]() shown in Fig. 3.5 with dimensions
shown in Fig. 3.5 with dimensions ![]() respectively, where the thickness of the line
corresponds to the strength of the current.
respectively, where the thickness of the line
corresponds to the strength of the current.
![\begin{figure}
\center
\includegraphics [width=5.0in,height=4.0in]{images/fractal_struc.eps}\end{figure}](img231.gif) |
The emission patterns along the cross-section x=10 km, averaged over the
duration of the discharge using Eq. (3.1) is shown in the four
panels of Fig 3.6. The velocity of the discharge was taken as ![]() and the amount current as Io=200 kA. The emission rate, e.g.
number of photons per cc per second, is computed in dB with respect to the
averaged emission rate over the image area.
and the amount current as Io=200 kA. The emission rate, e.g.
number of photons per cc per second, is computed in dB with respect to the
averaged emission rate over the image area.
The maximum intensity in kR for a optimal column integration along the x
axis, is shown in Fig. 3.7 as a function of the dimension of the
discharge ![]() . Since the optical emission intensity is extremely
sensitive to the power density, a factor of 2 on the electric field strength
can have profound effects on the emission pattern of a given fractal
discharge. Hence the sensitivity of the optical emission pattern on the
dimension of the discharge.
. Since the optical emission intensity is extremely
sensitive to the power density, a factor of 2 on the electric field strength
can have profound effects on the emission pattern of a given fractal
discharge. Hence the sensitivity of the optical emission pattern on the
dimension of the discharge.
![\begin{figure}
\center
\includegraphics [width=4in,height=2in]{images/emid.eps}\end{figure}](img233.gif) |
![\begin{figure}
\center
\includegraphics [width=5in,height=3in]{images/fractal_emi_Io.eps}\end{figure}](img235.gif) |
As seen in Fig. 3.6 different fractals require different current
peaks (or propagation speed) to produce similar emissions intensities. For
the 4 fractals of Fig. 3.6 we find the necessary current peak Io
needed to produce an emission intensity of about 100 kR. The corresponding
emission patterns are shown in Fig. 3.8 with their peak current Io. We note that the emission pattern corresponding to the fractal ![]() has considerable spatial structure as compared with the other cases in the
figure. We see that by having a spatially structured radiation pattern, the
fractals can increase the power density locally in specific regions of the
ionosphere and generate considerable optical emissions with relatively low
(more realistic) lightning discharge parameters.
has considerable spatial structure as compared with the other cases in the
figure. We see that by having a spatially structured radiation pattern, the
fractals can increase the power density locally in specific regions of the
ionosphere and generate considerable optical emissions with relatively low
(more realistic) lightning discharge parameters.
We have generated a novel model of red sprites that relies on the fractal
structure of the lightning discharge. Such fractal structure is reflected in
the fine structure of the subsequent optical emission pattern. The
incorporation of the fractal structure of lightning provides a clear method
for the generation of the fine structure of red sprites. For an optimal
configuration, so that the fields get projected upwards, the lightning
discharge must be horizontal, i.e. the so called intracloud lightning or
''spider lightning'' [Lyons, 1994]. It is important to notice that in
our model with ![]() the ionization starts occurring for Io>200
kA (i.e. for Io>200 kA the equation for the evolution of the electron
density ne should be included).
the ionization starts occurring for Io>200
kA (i.e. for Io>200 kA the equation for the evolution of the electron
density ne should be included).
We can compare these results with the simple tortuous random walk models (see Section 2.2.2). The maximum field strength at x=10 km y=10 km, z=60 km is shown in Fig. 2.20a and the emission strength in Fig. 2.20b as a function of the pathlength or dimension.
Therefore, we can obtain a significant increase in the strength of the radiated fields by treating the discharge as a fractal. Factors of 5 in the power density are not rare.
![\begin{figure}
\center
\includegraphics [width=4in,height=4in]{images/emi_walk_s.eps}\end{figure}](img236.gif) |
Certain fractals can radiate more effectively than others, but in general
this problem is very complicated. The power density, and thus the emission
pattern and intensity, scales as ![]() , where
, where ![]() is the efficiency
function of the different fractals.
is the efficiency
function of the different fractals. ![]() represent
the spatial structure of the radiation pattern with
represent
the spatial structure of the radiation pattern with ![]() as the angular
position. There is some dependence in the radiation fields as a function of
as the angular
position. There is some dependence in the radiation fields as a function of ![]() as can be observed from Fig. 2.22. Clearly, Q,
as can be observed from Fig. 2.22. Clearly, Q, ![]() , Io, D are the relevant parameters that control the optical emission
pattern and intensity.
, Io, D are the relevant parameters that control the optical emission
pattern and intensity.
Statistics of intracloud lightning are in the best cases incomplete, but
information about some independent measurements can be found in the book by
Uman [1987]. It seems to suggest that in extreme cases the intracloud
discharge can reach ![]() C or 100 kA, with a length of 10s of kms.
Some rough estimates can be made of the relevance of the model discharge
parameters by comparing with the statistics of cloud-to-ground discharges
given in Uman [1987].
C or 100 kA, with a length of 10s of kms.
Some rough estimates can be made of the relevance of the model discharge
parameters by comparing with the statistics of cloud-to-ground discharges
given in Uman [1987].
Such estimates can be made more precise if we assume the qualitative
model suggested by Lyons [1996] where the sprite generating +CGs
are associated with intracloud spider or dendritic lightning known to
accompany many +CG events. He presents a qualitative model which is
based on the fact that horizontal discharges of the order of 100 km
have been observed in connection with +CG events. The model starts with
the initial spider lightning followed by the positive leader toward
ground, which in turn is followed by the positive return stroke. The
latter generates an intracloud lightning discharge which propagates
along the (fractal) spider channel. Therefore, in this model, the
statistics of +CG current amplitudes could be related to the particular
intracloud events responsible for the sprite generation. In
cloud-to-ground discharges, a current peak of ![]() kA,
consistent with a charge transfer of Q=100 C, occurs between 1-5
% of the time. The speed of propagation of a cloud-to-ground is about
kA,
consistent with a charge transfer of Q=100 C, occurs between 1-5
% of the time. The speed of propagation of a cloud-to-ground is about
![]() , but intracloud discharges seem to propagate with
speeds of an order of magnitude smaller [Uman, 1987]. Consequently, our
model discharge parameters seem to agree with the sprite occurrence
[Lyons, 1994] and the statistics of lightning discharge
parameters [Uman, 1987].
, but intracloud discharges seem to propagate with
speeds of an order of magnitude smaller [Uman, 1987]. Consequently, our
model discharge parameters seem to agree with the sprite occurrence
[Lyons, 1994] and the statistics of lightning discharge
parameters [Uman, 1987].
We live in a world where dielectric discharges seem to have ![]() [
Sanders 1986, Niemeyer et al., 1984]. On the other hand
lightning discharges seem to show lower dimensions, a fact that might become
relevant due to the sensitivity of the emission strength on the fractal
dimension of the discharge. The optimal emissions intensity is obtained for
dimensions
[
Sanders 1986, Niemeyer et al., 1984]. On the other hand
lightning discharges seem to show lower dimensions, a fact that might become
relevant due to the sensitivity of the emission strength on the fractal
dimension of the discharge. The optimal emissions intensity is obtained for
dimensions ![]() for the fractal models used above.
for the fractal models used above.