For the purposes of this work, we assume that a fractal antenna can be formed as an array of ''small'' line elements having a fractal distribution in space. Such description is consistent with our understanding of fractal discharges and lightning observations as discussed by LeVine and Meneghini [1978], Niemeyer et al. [1984], Sander [1986], Williams [1988], and Lyons [1994]. Appendix A develops the theory for the calculation of the fields produced by a fractal antenna composed of small line elements and for the calculation of the array factor in the far field of the fractal.
Fractals are characterized by their dimension. It is the key structural
parameter describing the fractal and is defined by partitioning the volume
where the fractal lies into boxes of side ![]() . We hope that over
a few decades in
. We hope that over
a few decades in ![]() , the number of boxes that contain at least
one of the discharge elements will scale as
, the number of boxes that contain at least
one of the discharge elements will scale as ![]() . It is easy to verify that a point will have D=0, a line will have D=1 and a compact surface will have D=2 . The box counting dimension [Ott, 1993] is then defined by
. It is easy to verify that a point will have D=0, a line will have D=1 and a compact surface will have D=2 . The box counting dimension [Ott, 1993] is then defined by
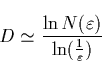 |
(1) |
To understand the concept of a fractal antenna, we start with a long line antenna which radiates as a dipole (top of Fig. 2.1). Then we make the antenna path tortuous (middle of Fig. 2.1), essentially generating a two dimensional phased array. The resulting tortuous (fractal) antennae can then be considered as a non uniform distribution of radiating elements (bottom of Fig. 2.1). The radiation pattern will exhibit an antenna gain if the radiating elements radiate, at least partially, coherently.
![\begin{figure}
\center
\includegraphics [width=2.5in,height=1.5in]{images/alpha_diagram.eps}\end{figure}](img24.gif) |
Each of the elements contributes to the total radiated power density at a given point with a vectorial amplitude and phase, i.e.
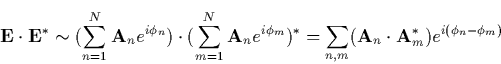 |
(2) |
In the sense of statistical optics, we can consider the ensemble average of
Eq. (2.2), using an ergodic principle, over the spatial
distribution ![]() of the fractal elements [Goodman, 1985]. For simplicity we
assume that the distributions for each of the elements are independent, and
also the same, hence
of the fractal elements [Goodman, 1985]. For simplicity we
assume that the distributions for each of the elements are independent, and
also the same, hence
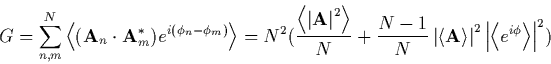
By requiring that ![]() we obtain that the
ensemble average is
we obtain that the
ensemble average is
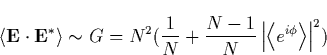
If the distribution of the vector amplitudes does not satisfy the above
relations, e.g. the radiators are oriented in arbitrary directions, then the
power density will be less coherent due to ![]() . A similar result can be achieved by having a power law
distribution in the amplitudes. In conclusion, the radiation field from a
power law distribution of phases will have a point where the phases from the
radiators will add up almost (partially) coherently showing a significant
gain over a random distribution of phases.
. A similar result can be achieved by having a power law
distribution in the amplitudes. In conclusion, the radiation field from a
power law distribution of phases will have a point where the phases from the
radiators will add up almost (partially) coherently showing a significant
gain over a random distribution of phases.
The parameter ![]() is related to the fractal dimension D [Ott,
1993] of the antenna. We conjecture that the most relevant structural
parameter in determining the radiation pattern from a fractal antenna is its
fractal dimension. The fractal dimension will be an important
parametrization for the fractal models that we will explore later, and will
impact significantly on the intensity and spatial structure of the radiated
pattern. The partial coherence of the radiators depends on the spatial power
law distribution.
is related to the fractal dimension D [Ott,
1993] of the antenna. We conjecture that the most relevant structural
parameter in determining the radiation pattern from a fractal antenna is its
fractal dimension. The fractal dimension will be an important
parametrization for the fractal models that we will explore later, and will
impact significantly on the intensity and spatial structure of the radiated
pattern. The partial coherence of the radiators depends on the spatial power
law distribution.
Such a power law distribution of phases can be visualized with the help of
Cantor sets [Ott, 1993]. A family of Cantor sets is constructed by
successively removing the middle ![]() fraction from an interval, taken
as [0,1], and repeating the procedure to the remaining intervals (see Fig.
2.3). At the nth step, a radiator is placed at the mid-point
of each of the remaining intervals.
fraction from an interval, taken
as [0,1], and repeating the procedure to the remaining intervals (see Fig.
2.3). At the nth step, a radiator is placed at the mid-point
of each of the remaining intervals.
Note that for ![]() we obtain a uniform distribution of elements, but
for
we obtain a uniform distribution of elements, but
for ![]() the radiators are non-uniformly distributed, and in fact
the spatial distribution follows a power law that can be described by its
fractal dimension. Suppose that for
the radiators are non-uniformly distributed, and in fact
the spatial distribution follows a power law that can be described by its
fractal dimension. Suppose that for ![]() we require
we require ![]() intervals to cover the fractal, then it is clear that with
intervals to cover the fractal, then it is clear that with ![]() we would require
we would require ![]() intervals to cover the fractal. But the
fractal is the same, therefore,
intervals to cover the fractal. But the
fractal is the same, therefore, ![]() . From the scaling
. From the scaling ![]() we obtain
that the dimension is given by
we obtain
that the dimension is given by
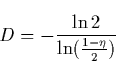
We can go further, and write a formula for the radiation field due to the ![]() Cantor set of radiators. Note that if at the nth step we have
the radiators placed at the sequence of points
Cantor set of radiators. Note that if at the nth step we have
the radiators placed at the sequence of points ![]() then at the nth+1 step each radiator at xi will be replaced by two
radiators at
then at the nth+1 step each radiator at xi will be replaced by two
radiators at ![]() generating
the sequence
generating
the sequence ![]() . Since we start with
. Since we start with ![]() the sequences Sn at the nth step are trivially constructed.
The radiation field (see Eq. (2.1)) from this
the sequences Sn at the nth step are trivially constructed.
The radiation field (see Eq. (2.1)) from this ![]() Cantor set
at the nth step can then be written as
Cantor set
at the nth step can then be written as
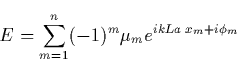 |
(3) |
The space dependence of the radiation fields is plotted in Fig. (2.4)a-b for ![]() (D=0.63) and
(D=0.63) and ![]() (D=1)
respectively, where the sets have been taken to the 5th level. The most
relevant issue for our purposes is the fact that there is a direction at
which phases add coherently (partially) for
(D=1)
respectively, where the sets have been taken to the 5th level. The most
relevant issue for our purposes is the fact that there is a direction at
which phases add coherently (partially) for ![]() while this does not
happen for the homogeneous case
while this does not
happen for the homogeneous case ![]() .
.
Therefore, partial coherence occurs naturally in systems that have power-law spatial distributions. We are now ready to turn to the properties of fractal antennae with propagating currents. Specifically, how tortuosity and branching can increase the radiated field intensity in some locations as compared with single dipole antennae.
To illustrate the properties of fractal antennae compared to those of simple
dipole radiators, we take the fractal antenna as composed of small line
elements and compute its far field radiation pattern. For an oscillating
current ![]() that propagates with speed
that propagates with speed ![]() v/c
along the antenna, the contribution from each line element to the total
radiation field is (from Eq. (2.1))
v/c
along the antenna, the contribution from each line element to the total
radiation field is (from Eq. (2.1))
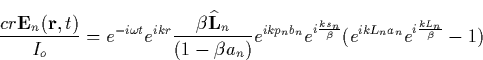 |
(4) |
In general, the radiation pattern of an antenna can be effectively excited,
only by certain frequencies corresponding to the characteristic length
scales of the antenna, e.g. ![]() (see Eq. (2.4)). Therefore,
if there is no characteristic size, as in the case of a power law structure,
then the antenna will generate an effective radiation pattern for a whole
range of frequencies controlled by the smaller and largest spatial scale.
Such antenna is called a broad band antenna, and that is why fractal
antennae are so important in many applications.
(see Eq. (2.4)). Therefore,
if there is no characteristic size, as in the case of a power law structure,
then the antenna will generate an effective radiation pattern for a whole
range of frequencies controlled by the smaller and largest spatial scale.
Such antenna is called a broad band antenna, and that is why fractal
antennae are so important in many applications.
By spatially superposing these line radiators we can study the properties of simple fractal antennae. Of special interest, to our high altitude lightning work, is to compare the radiation pattern of these fractal models with a simple (meaning one line element) dipole antenna.
The first element in understanding fractal antennae is the concept of
tortuosity in which the path length between two points is increased by
requiring that the small line elements are no longer colinear. A simple
tortuous model is displayed in Fig. 2.5, where the parameter ![]() represents the variation from the simple dipole model (line
radiator), i.e. the dipole is recovered as
represents the variation from the simple dipole model (line
radiator), i.e. the dipole is recovered as ![]() .
.
![\begin{figure}
\center
\includegraphics [width=4in]{images/diagram_torto.eps}\end{figure}](img75.gif) |
Except for the propagation effect, we can observe that this antenna (Fig. 2.5) can be considered as the contribution from a long line element (a dipole) plus the contribution from a Cantor set of radiators as described in the previous section (see Eq. (2.3)). Therefore, the tortuosity naturally increases the radiation field intensity, at least in some direction, as compared with the single dipole element.
The field can be written for the structure of 2.5, with the help of Eq. (2.4), as the superposition of the 2N line elements, and is given by the normalized field
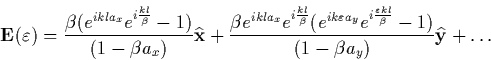 |
(5) |
For our purposes, the most important contribution comes from the fact that ![]() is essentially independent of N and it
scales as
is essentially independent of N and it
scales as ![]() which
corresponds to the increase in the path length of the antenna due to the
tortuosity. Such technique can be applied to other geometries, giving
essentially the same scaling
which
corresponds to the increase in the path length of the antenna due to the
tortuosity. Such technique can be applied to other geometries, giving
essentially the same scaling ![]() result.
This fact will be extremely relevant in our analysis since lightning has
naturally a tortuous path.
result.
This fact will be extremely relevant in our analysis since lightning has
naturally a tortuous path.
More generally, a fractal tortuous path can also be constructed in terms of
a random walk between two endpoints [Vecchi, et al., 1994]. We start
with a straight line of length L, to which the midpoint is displaced using
a Gaussian random generator with zero average and deviation ![]() (usually
(usually ![]() ). The procedure is then repeated to each of the
straight segments N times. There is a clear repetition in successive halving
of the structure as we go to smaller scales, making this antenna broad band.
Figure 2.6a shows a typical tortuous fractal where the division
has been taken to the N=8 level and in which the pathlength s has increased
5 times, i.e. s=5L. We can estimate the fractal dimension by realizing
that the total length should go as
). The procedure is then repeated to each of the
straight segments N times. There is a clear repetition in successive halving
of the structure as we go to smaller scales, making this antenna broad band.
Figure 2.6a shows a typical tortuous fractal where the division
has been taken to the N=8 level and in which the pathlength s has increased
5 times, i.e. s=5L. We can estimate the fractal dimension by realizing
that the total length should go as ![]() , where
, where ![]() is the
average segment size. This formulation is completely equivalent to Eq. (2.1).
is the
average segment size. This formulation is completely equivalent to Eq. (2.1).
We let an oscillating current, e.g. ![]() propagate along the
fractal, but in real applications we can imagine the oscillating current
lasting for only a finite time
propagate along the
fractal, but in real applications we can imagine the oscillating current
lasting for only a finite time ![]() . In order to have a finite
current pulse propagating through the fractal random walk, we let
. In order to have a finite
current pulse propagating through the fractal random walk, we let ![]() with
with ![]() and
and ![]() as the step function. Here nf
represent the number of oscillations during the decay time scale 1/
as the step function. Here nf
represent the number of oscillations during the decay time scale 1/![]() . We chose the decay parameters as
. We chose the decay parameters as ![]() s-1 and
s-1 and ![]() s-1, hence
s-1, hence ![]() , which correspond to
realistic parameters for lightning [Uman, 1987]. The radiated power
density is then computed using Eq. (A.4) and is shown in Fig. 2.6b for nf=5 and
, which correspond to
realistic parameters for lightning [Uman, 1987]. The radiated power
density is then computed using Eq. (A.4) and is shown in Fig. 2.6b for nf=5 and ![]() at the position ax=0, ay=0, r=60 km. The dipole equivalent is given by the dashed lines in all 3
panels. The peak in the radiated power density is about 10 times larger than
for the dipole case, which agrees well with the results
at the position ax=0, ay=0, r=60 km. The dipole equivalent is given by the dashed lines in all 3
panels. The peak in the radiated power density is about 10 times larger than
for the dipole case, which agrees well with the results ![]()
![]() n
n![]() even though the effect from the tortuosity is not
small. The larger path length of the tortuous discharge produces an increase
in the radiation as compared with a dipole radiator. Of course there is a
limit due to energy conservation, but in practical applications we are well
under it. The increase in the high frequency components of the radiated
field power spectrum (Fig. 2.6c), as compared with the dipole
antenna, will be responsible for the spatially structured radiation pattern.
even though the effect from the tortuosity is not
small. The larger path length of the tortuous discharge produces an increase
in the radiation as compared with a dipole radiator. Of course there is a
limit due to energy conservation, but in practical applications we are well
under it. The increase in the high frequency components of the radiated
field power spectrum (Fig. 2.6c), as compared with the dipole
antenna, will be responsible for the spatially structured radiation pattern.
![\begin{figure}
\center
\includegraphics [width=6in,height=3in]{images/f-2-2-2.eps}\end{figure}](img105.gif) |
The far field array factor ![]() (defined in Appendix
A) and the peak power density depend on the path length, or equivalently on
the number N of divisions of the fractal. Figure 2.7b shows the
array factor as a function of the path length for the fractal shown in Fig.
2.7a. Here nf=5 so that the peak of the array factor is at ax=0 and ay=0. There is a clear increase in the array factor from the
tortuous fractal as compared with the single dipole.
(defined in Appendix
A) and the peak power density depend on the path length, or equivalently on
the number N of divisions of the fractal. Figure 2.7b shows the
array factor as a function of the path length for the fractal shown in Fig.
2.7a. Here nf=5 so that the peak of the array factor is at ax=0 and ay=0. There is a clear increase in the array factor from the
tortuous fractal as compared with the single dipole.
![\begin{figure}
\center
\includegraphics [width=6in,height=3in]{images/f-2-2-3.eps}\end{figure}](img107.gif) |
Another important concept related to fractal antennae is the spatial
structure of the radiation field. We can see from the array factor, Eq. (A.5), that for large nf ![]() . The spatial dependence of the array factor will be
determined by the factor
. The spatial dependence of the array factor will be
determined by the factor ![]() over the fractal.
Consequently, the radiation pattern will have spatial structure when
over the fractal.
Consequently, the radiation pattern will have spatial structure when ![]() which translate into nf>50. Figure 2.8b shows the array factor at the height h=60 km for the discharge
structure shown in Fig. 2.8a with nf=200. Therefore, such a
tortuous fractal can also display a spatial structure in the radiation
pattern. But it is more natural for the spatial structure to be generated
through a branching process as we will see in the next section.
which translate into nf>50. Figure 2.8b shows the array factor at the height h=60 km for the discharge
structure shown in Fig. 2.8a with nf=200. Therefore, such a
tortuous fractal can also display a spatial structure in the radiation
pattern. But it is more natural for the spatial structure to be generated
through a branching process as we will see in the next section.
![\begin{figure}
\center
\includegraphics [width=6in,height=4in]{images/f-2-2-6.1.eps}\end{figure}](img111.gif) |
There is an energy constraint that limits the degree of tortuosity of a fractal lightning discharge since we cannot radiate more energy than what is initially stored as separated charge. Also, if the line elements of the antenna given by Fig. 2.5 get too close together, then their contribution to the radiated field will tend to cancel each other. Therefore, there is an optimal number of elements forming an antenna, and this optimal number translates into an optimal dimension of the fractal, more on this later.
Another element in understanding fractal antennae is the concept of
branching. Take the simple branching element shown in Fig. 2.9
where the current is divided between the two branching elements. We can
compute the radiation field, for a propagating current I![]() ,as
,as
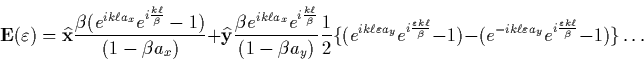 |
(6) |
![\begin{figure}
\center
\includegraphics [width=4in,height=2in]{images/f-2-2-4.eps}\end{figure}](img115.gif) |
Again, the analysis can be simplified in the limit for small ![]() ,i.e.
,i.e. ![]() . Of course P(0) is the dipole contribution, and
. Of course P(0) is the dipole contribution, and ![]() is the change in the radiated power density due to the
line branching. The dipole has a maximum in the radiated power density
is the change in the radiated power density due to the
line branching. The dipole has a maximum in the radiated power density ![]() , while the branching
contribution goes as
, while the branching
contribution goes as ![]() . The function
f depends on the given parameters, but its maximum is of the order
. The function
f depends on the given parameters, but its maximum is of the order ![]() with clear regions in (ax,ay) where it is positive. Therefore,
the branching process can give rise to an increase in the radiated power
density at certain position. Of course this increase is due to the increase
in the path length. This effect will saturate as
with clear regions in (ax,ay) where it is positive. Therefore,
the branching process can give rise to an increase in the radiated power
density at certain position. Of course this increase is due to the increase
in the path length. This effect will saturate as ![]() is increased
passed one, since then the strongest contribution will come from the dipole
radiator given by 2
is increased
passed one, since then the strongest contribution will come from the dipole
radiator given by 2![]() .
.
A interesting and manageable broadband antenna can be described in terms of
the Weierstrass functions [Werner and Werner, 1995]. We take
successive branching elements, as shown in Fig. 2.10a, where we
distribute the current at each branching point so that the branching element
keeps a fraction ![]() of the current. The nth branching element is
displaced by a factor
of the current. The nth branching element is
displaced by a factor ![]() with respect to the origin. If we
concentrate only on the contribution from the last branching set, as shown
in Fig. 2.10a, we can write the field as
with respect to the origin. If we
concentrate only on the contribution from the last branching set, as shown
in Fig. 2.10a, we can write the field as
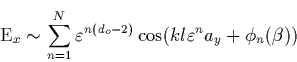
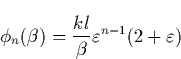
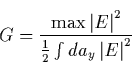
![\begin{figure}
\center
\includegraphics [width=4in,height=4.0in]{images/f-2-2-5.eps}\end{figure}](img129.gif) |
Note the increase in the gain as a function of dimension. In general, there
is an optimal value of D that generates the highest power density and that
does not necessarily has to be for D=2. In Fig. 2.10b all the
elements from the antenna add up coherently at ay=0, hence providing
perfect coherence. For a finite ![]() the propagation brings a
different phase shift at each element. Figure 2.10d shows the
effect for
the propagation brings a
different phase shift at each element. Figure 2.10d shows the
effect for ![]() as a function of
as a function of ![]() . Note that at no point
there is perfect coherence, but there is clear partial coherence. The peak
value of E2 is actually sensitive to
. Note that at no point
there is perfect coherence, but there is clear partial coherence. The peak
value of E2 is actually sensitive to ![]() .
.
Even though fractal antennae naturally lead to the concept of an increase in the peak radiated power, it also has a second important consequence due to branching. As we have seen in the case of the Wiertrauss function, fractal antennae naturally result in the generation of a spatial structure in the radiated power density. This interplay between the spatial structure and the increase in the peak radiated power are the essential ingredients of fractal antennae and why they are so important. A clear example can be illustrated in Fig. 2.10d where there are multiple relevant peaks of the radiated power in space.
Fractal Antenna/Field Gain simple fractal antenna examples gain due to tortuosity + branching
The hypothesis of this work is that the structure of the red sprites can be attributed to the fact that the power density generated by lightning does not have the smooth characteristics expected from the dipole model of Eq. 2.7, but the structured form expected from a fractal antenna [ Kim and Jaggard, 1986; Werner et al., 1995]. Previous studies of lightning assumed that the RF fields causing the atmospheric heating and emissions, were produced by an horizontal dipole cloud discharge moment M that generates an electric field at the height z, given by
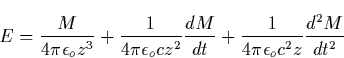 |
(7) |
It is obvious that such a horizontal dipole results in electric fields that
vary smoothly with distance. However, it is well known that lightning
discharges follow a tortuous path [LeVine and Meneghini, 1978]. It was
shown [ Williams, 1988] that intracloud discharges resemble the well
known Lichtenberg patterns observed in dielectric breakdown. In fact a
time-integrated photograph of a surface leader discharge is illustrated by
Figure 2.11 . These patterns have been recently identified as fractal
structures of the Diffusion Limited Aggregate (DLA) type with a fractal
dimension ![]() [Sander, 1986; Niemeyer et al., 1984].
[Sander, 1986; Niemeyer et al., 1984].
![\begin{figure}
\center
\includegraphics [width=3in]{images/lichtenberg.eps}\end{figure}](img135.gif) |
As noted previously, the tortuous path increase the effective dipole moment,
since now the pathlength along the discharge is longer that the Euclidean
distance. To understand this analogy, we construct a tortuous walk between
two points separated by a distance R as shown in Fig 2.12. Take the
tortuous path as N small steps of averaged step length ![]() , then the
total path length S along the tortuous discharge is
, then the
total path length S along the tortuous discharge is
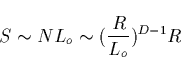
This is only an analogy, but it gives us good intuition that a fractal
lightning discharge will produce an increase in the radiated field
intensity, at least locally, as compared with a dipole model and a spatially
structured radiation pattern. A fractal dielectric discharge of size R can
be modeled as a set of non-uniformly distributed small current line elements
[ Niemeyer et al., 1984] that represent the steps of the discharge
breakdown as it propagates during an intracloud lightning discharge. The
size of the elementary current steps is about ![]() m [Uman,
1987]. As a current pulse propagates along this horizontal fractal discharge
pattern it radiates energy upwards (see Appendix A on how the fields are
calculated) as well as downward.
m [Uman,
1987]. As a current pulse propagates along this horizontal fractal discharge
pattern it radiates energy upwards (see Appendix A on how the fields are
calculated) as well as downward.
To determine the extent over which the non-uniformity of the lightning discharge current affects the power density structure projected in the lower ionosphere, we will now construct a simple fractal model of the lightning discharge that will yield a spatio-temporal radiation pattern at the relevant heights.
We want to generate a fractal model that can be parametrized by its fractal
dimension. For this purpose, we follow Niemeyer et al. [1984] who
proposed a two dimensional stochastic dielectric discharge model that
naturally leads to fractal structures. In this model the fractal dimension D
can be easily parametrized by a parameter ![]() . Femia et al. [1993] found
experimentally that the propagating stochastic Lichtenberg pattern is
approximately an equipotential. Then, the idea is to create a discrete
discharge pattern that grows stepwise by adding an adjacent grid point to
the discharge pattern generating a new bond. The new grid point, being part
of the discharge structure, will have the same potential as the discharge
pattern. Such local change will affect the global potential configuration,
see Fig. 2.13.
. Femia et al. [1993] found
experimentally that the propagating stochastic Lichtenberg pattern is
approximately an equipotential. Then, the idea is to create a discrete
discharge pattern that grows stepwise by adding an adjacent grid point to
the discharge pattern generating a new bond. The new grid point, being part
of the discharge structure, will have the same potential as the discharge
pattern. Such local change will affect the global potential configuration,
see Fig. 2.13.
The potential for the points not on the discharge structure is calculated by iterating the discrete two dimensional Laplace's equation
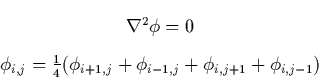
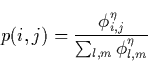
The color coding corresponds to the potential. Figure 2.15 shows a
plot of ![]() vs.
vs. ![]() for the fractal discharge
of Fig. 2.14, i.e.
for the fractal discharge
of Fig. 2.14, i.e. ![]() . Again the scaling behavior only
occurs over a few decades, but it is very clear. The dimension of this
structure is
. Again the scaling behavior only
occurs over a few decades, but it is very clear. The dimension of this
structure is ![]() .
.
Note that this model, and also the dimension of the discharge, is
parametrized by ![]() . Intuitively we expect that when
. Intuitively we expect that when ![]() the
discharge will have the same probability of propagating in any direction,
therefore, the discharge will be a compact structure with a dimension D=2.
If
the
discharge will have the same probability of propagating in any direction,
therefore, the discharge will be a compact structure with a dimension D=2.
If ![]() then the discharge will go in only one
direction, hence D=1. Between these two limits, the dimension will be the
function
then the discharge will go in only one
direction, hence D=1. Between these two limits, the dimension will be the
function ![]() shown in Fig 2.16. As an example the
corresponding structure generated for
shown in Fig 2.16. As an example the
corresponding structure generated for ![]() (Fig 2.17) has a
dimension of D=1.2.
(Fig 2.17) has a
dimension of D=1.2.
To compute the radiated fields, we must describe the current along each of
the segments of the fractal discharge. We start with a charge Qo at the
center of the discharge. The current is then discharged along each of the
dendritic arms. At each branching point we chose to ensure conservation of
current, but intuitively we know that a larger fraction of the current will
propagate along the longest arm. Suppose that a current Io arrives at a
branching point, and if Li is the longest distance along the ith
branching arm, we intuitively expect that the current on the ith arm
should be proportional to ![]() . Therefore, we satisfy charge (or
current) conservation if the current along the ith branching arm is
. Therefore, we satisfy charge (or
current) conservation if the current along the ith branching arm is
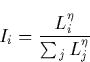
A current pulse propagates along the horizontal (in the x-y plane) 2
dimensional fractal discharge structure, e.g. ![]() generating radiation fields. The radiation field is the superposition, with
the respective phases, of the small line current elements. The intracloud
current pulse is taken as a series of train pulses that propagate along the
arms of the antenna
generating radiation fields. The radiation field is the superposition, with
the respective phases, of the small line current elements. The intracloud
current pulse is taken as a series of train pulses that propagate along the
arms of the antenna
![]()
On a given position the time dependence of the field intensity E2 has a
fractal structure, as it is shown in Fig. 2.18a for the stochastic
discharge model with ![]() . The frequency spectrum of the electric field
is shown in Fig. 2.18b. It is very important to realize that the
relevant frequencies are below a few hundred kHz. By restricting the field
frequencies to below a few hundred kHz, the analysis is greatly simplified,
since then the conductivity and dielectric tensors can be considered as
independent of time in the lower ionosphere (see Appendix B).
. The frequency spectrum of the electric field
is shown in Fig. 2.18b. It is very important to realize that the
relevant frequencies are below a few hundred kHz. By restricting the field
frequencies to below a few hundred kHz, the analysis is greatly simplified,
since then the conductivity and dielectric tensors can be considered as
independent of time in the lower ionosphere (see Appendix B).
The large conductivity of the ground at these frequencies can be included by
assuming to first order an image discharge of opposite current below a
perfectly conductive plane. The primary discharge is taken to be at zo=5
km above the ground. This parameter is not very relevant, since we are
interested in the field at heights of about ![]() km, therefore, moving
the discharge from 5 to 10 km will only change the field strength by a
marginal 10%.
km, therefore, moving
the discharge from 5 to 10 km will only change the field strength by a
marginal 10%.
![\begin{figure}
\center
\includegraphics [width=4in]{images/field_in_t.eps}\end{figure}](img172.gif) |
For a 2-dimensional fractal structure, we expect that the strength of the radiated power density depends on the fractal structure, i.e. its fractal dimension. If the strength of the k Fourier component is Ak then the field in the far field [ Jackson 1975] at r along the axis of the fractal will be given by
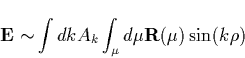
The cross section of the fractal at a given radius ![]() will resemble a
Cantor set in
will resemble a
Cantor set in ![]() , and the phase contribution will
be given by
, and the phase contribution will
be given by ![]() which will
be finite for an asymmetrical fractal. The integration can be carried as a
Lebesgue integral or as a Riemann-Stieltjes integral over this pseudo-Cantor
set [Royden, 1963]. Note that if the fractal is uniformly distributed
along
which will
be finite for an asymmetrical fractal. The integration can be carried as a
Lebesgue integral or as a Riemann-Stieltjes integral over this pseudo-Cantor
set [Royden, 1963]. Note that if the fractal is uniformly distributed
along ![]() , corresponding to D=2, then
, corresponding to D=2, then ![]() . Similarly,
for a delta function at
. Similarly,
for a delta function at ![]() corresponding to D=1,
corresponding to D=1, ![]() gives a positive contribution.
gives a positive contribution. ![]() is a very complicated
function that depends on the details of the current distribution along the
fractal. In an average sense we can suppose that
is a very complicated
function that depends on the details of the current distribution along the
fractal. In an average sense we can suppose that ![]() where f(D=1)=1 and f(D=2)=0 but f can be greater than one for other values as
has been investigated in previous sections when branching and propagation
occurs. Therefore,
where f(D=1)=1 and f(D=2)=0 but f can be greater than one for other values as
has been investigated in previous sections when branching and propagation
occurs. Therefore,
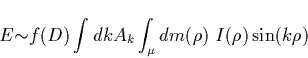
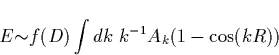
| |
(8) |
On the other hand, the Rayleigh length, the distance beyond which the field
start decaying to their far field values, behaves as ![]() for a given
for a given ![]() . Red sprites
occur at a height
. Red sprites
occur at a height ![]() km, therefore, for
km, therefore, for ![]() elements with sizes smaller than
elements with sizes smaller than ![]() do not contribute to the
field, i.e. as we increase z we wash out the information of increasingly
larger spatial scales of the fractal. It is the power law dependence, as
specified by the fractal dimension, that determine the field pattern.
do not contribute to the
field, i.e. as we increase z we wash out the information of increasingly
larger spatial scales of the fractal. It is the power law dependence, as
specified by the fractal dimension, that determine the field pattern.
Even though, the radiation pattern will depend on the details of the fractal
structure, we expect that the most relevant parameter in determining the
radiation pattern will be the fractal dimension, as found by Myers et al.
[1990] for simple fractals. There is an interplay between the dimension and
the spatial structure of the radiation pattern. For a dimension close to ![]() or
or ![]() , there will be no significant spatial structure. While
an intermediate dimension can produce a significant spatial structure.
, there will be no significant spatial structure. While
an intermediate dimension can produce a significant spatial structure.
First we start by computing the array factor based on the far field
approximation (see Appendix A). We take n![]() and
and ![]() and
compute the array factor at a height z=60 km. Figure 2.19 shows the
array factor for the discharge structure shown in Fig. 2.17 with
and
compute the array factor at a height z=60 km. Figure 2.19 shows the
array factor for the discharge structure shown in Fig. 2.17 with ![]() .
.
The length of the elementary current elements is about 100 m. The array
factor shows clear structure. A cross-section of the normalized array factor
are shown in Fig. 2.20 and Fig. 2.21 for ![]() and
and ![]() respectively.
respectively.
![\begin{figure}
\begin{minipage}[b]
{.45\linewidth}
\centering
\includegraphics...
...graphics [width=2.5in,height=2in]{images/array2.0.eps}\end{minipage}\end{figure}](img205.gif) |
Similarly, the array factor at x=10 km, y=10 km, z=60 km is shown as a
function of the fractal dimension of the discharges for ![]() and
and ![]() in Fig. 2.22a for nf=0 and Fig. 2.22b
for nf=200.
in Fig. 2.22a for nf=0 and Fig. 2.22b
for nf=200.
![\begin{figure}
\center
\includegraphics [width=5.5in,height=2.0in]{images/array_d.eps}\end{figure}](img208.gif) |
The fractal dimension dependence of the array factor is very intriguing, but
is of clear significance for our lightning studies. What about the time
dependence of the radiations fields? Figure 2.23 shows the time
dependence of the radiation fields for ![]() with nf=200,50,1
where each figure is carefully labeled.
with nf=200,50,1
where each figure is carefully labeled.
![\begin{figure}
\center
\includegraphics [width=5.5in,height=5.5in]{images/field_tim_all.eps}\end{figure}](img210.gif) |
We take the case for ![]() and we study the dependence of the array
factor as a function of the current frequency as parametrized by nf.
Figure 2.24 shows the frequency dependence of the array factor at
this location x=10 km, y=10 km, z=60 km. Initially the array factor
increases linearly with nf as expected but then it starts to oscillate as
the spatial variation of the field pattern becomes relevant.
and we study the dependence of the array
factor as a function of the current frequency as parametrized by nf.
Figure 2.24 shows the frequency dependence of the array factor at
this location x=10 km, y=10 km, z=60 km. Initially the array factor
increases linearly with nf as expected but then it starts to oscillate as
the spatial variation of the field pattern becomes relevant.
In conclusion, the fractal nature of the discharges, being a simple random walk or a stochastic discharge model, leads naturally to an increase in the peak power density as compared with the dipole model. This increase is related to the increase in the antenna path length, or tortuosity, and on the branching process. It will be shown later that this gain in peak power density leads to a significant reductions in the discharge properties (e.g. charge, peak current) required to produce the observed sprite emissions.
In conclusion certain fractals can radiate more effectively than others, but
in general this problem is very complicated. The power density, and thus the
emission pattern and intensity, scales as ![]() , where
, where ![]() is the efficiency function of the different fractals.
is the efficiency function of the different fractals. ![]() represent the spatial structure of the radiation pattern with
represent the spatial structure of the radiation pattern with ![]() as the angular position.
as the angular position.